Тема 7. Спектр света.
Прямое и обратное преобразование Фурье для вещественной напряженности электрического поля в одной точке пространства имеют следующий вид
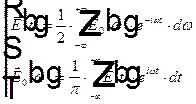 , здесь коэффициент
, здесь коэффициент 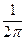 может быть разделен на два сомножителя в интегралах произвольным образом.
может быть разделен на два сомножителя в интегралах произвольным образом.
Вещественность 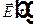 накладывает некоторые ограничения на вид ее Фурье образа
накладывает некоторые ограничения на вид ее Фурье образа 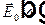 . И действительно, из вещественности
. И действительно, из вещественности 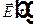 следует равенство
следует равенство 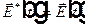 . Подставим в обе части равенства вместо величины
. Подставим в обе части равенства вместо величины 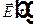 ее представление в виде Фурье интеграла и получим
ее представление в виде Фурье интеграла и получим 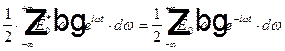 . Заменим в первом интеграле
. Заменим в первом интеграле 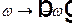 и перенесем все в правую часть равенства. Тогда получим
и перенесем все в правую часть равенства. Тогда получим
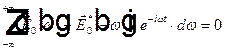 . Это равенство можно рассматривать, как Фурье разложение по частотам нуля, который стоит в правой части равенства. Из единственности разложения по частотам следует, что Фурье образ нуля должен быть тождественно нулем, тогда
. Это равенство можно рассматривать, как Фурье разложение по частотам нуля, который стоит в правой части равенства. Из единственности разложения по частотам следует, что Фурье образ нуля должен быть тождественно нулем, тогда 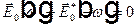 , откуда получаем
, откуда получаем 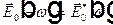 . То есть, Фурье образ поля
. То есть, Фурье образ поля 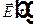 на отрицательных частотах может быть выражен, как комплексно сопряженная величина к Фурье образу на положительных частотах. Тогда Фурье интеграл по всем частотам можно выразить через Фурье интеграл только по положительным частотам.
на отрицательных частотах может быть выражен, как комплексно сопряженная величина к Фурье образу на положительных частотах. Тогда Фурье интеграл по всем частотам можно выразить через Фурье интеграл только по положительным частотам.
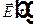 =
= 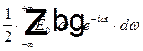 =
= 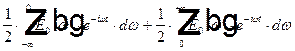
В первом интеграле заменим 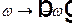 и воспользуемся равенством
и воспользуемся равенством 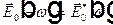 , тогда
, тогда 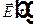 =
= 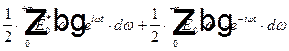 . Заметим, что первое слагаемое является комплексно сопряженным ко второму, тогда
. Заметим, что первое слагаемое является комплексно сопряженным ко второму, тогда
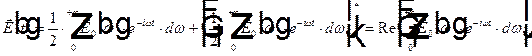 , так как при сложении комплексно сопряженных величин вещественная часть удваивается, а мнимая сокращается.
, так как при сложении комплексно сопряженных величин вещественная часть удваивается, а мнимая сокращается.
В результате получаем разложение вещественного электрического поля по всем частотам и по положительным частотам
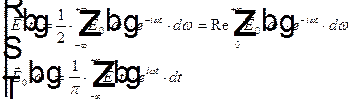 .
.
Комплексным полем можно считать выражение 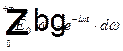 , если не брать от него вещественную часть. Величина
, если не брать от него вещественную часть. Величина 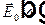 показывает, сколько в поле
показывает, сколько в поле 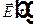 содержится сигнала с частотой
содержится сигнала с частотой 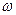 .
.
Обычно мы не знаем величину электрического поля на бесконечном временном интервале. В таком случае за пределами известного интервала времени 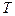 либо считают поле
либо считают поле 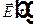 равным нулю, либо считают, что поле периодически повторяется с периодом
равным нулю, либо считают, что поле периодически повторяется с периодом 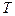 . Пусть поле
. Пусть поле 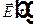 — периодическая функция времени. Тогда ее можно разложить в ряд Фурье по кратным частотам.
— периодическая функция времени. Тогда ее можно разложить в ряд Фурье по кратным частотам.
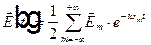 , где
, где 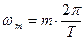 .
.
Из-за вещественности поля 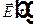 амплитуды разложения по отрицательным частотам, аналогично интегралу Фурье по отрицательным частотам, могут быть выражены, как комплексно сопряженные величины к амплитудам на положительных частотах
амплитуды разложения по отрицательным частотам, аналогично интегралу Фурье по отрицательным частотам, могут быть выражены, как комплексно сопряженные величины к амплитудам на положительных частотах 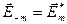 . В результате можно получить разложение поля как по частотам обоих знаков, так и только по положительным частотам.
. В результате можно получить разложение поля как по частотам обоих знаков, так и только по положительным частотам.
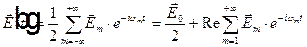
Если на левое равенство подействовать оператором 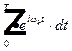 , где вместо жирной точки нужно подставить левую и правую часть равенства, то все слагаемые в правой части равенства кроме
, где вместо жирной точки нужно подставить левую и правую часть равенства, то все слагаемые в правой части равенства кроме 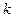 -ого слагаемого обнуляются в результате интегрирования. Откуда получаем амплитуды ряда Фурье
-ого слагаемого обнуляются в результате интегрирования. Откуда получаем амплитуды ряда Фурье 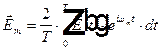 .
.
Окончательно для периодической функции 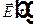 получаем представление в виде ряда Фурье
получаем представление в виде ряда Фурье
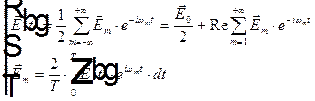
 2014-02-10
2014-02-10 526
526








