Рассмотрим систему 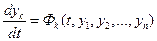 (k = 1,2,...,n) (1) с начальным условием
(k = 1,2,...,n) (1) с начальным условием 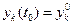 (k = 1,2,...,n), которое является результатом измерений и получено с некоторой погрешностью. Если сколь угодно малые изменения начальных данных способны сильно изменить решение, то такое решение не имеет никакого прикладного значения и даже приближенно не описывает изучаемое явление. Естественно возникает вопрос о нахождении условий, при которых достаточно малое изменение начальных данных вызывает сколь угодно малое изменение решения.
(k = 1,2,...,n), которое является результатом измерений и получено с некоторой погрешностью. Если сколь угодно малые изменения начальных данных способны сильно изменить решение, то такое решение не имеет никакого прикладного значения и даже приближенно не описывает изучаемое явление. Естественно возникает вопрос о нахождении условий, при которых достаточно малое изменение начальных данных вызывает сколь угодно малое изменение решения.
Если t меняется на конечном отрезке 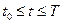 , то ответ уже получен теоремой о непрерывной зависимости решения от начальных значений.
, то ответ уже получен теоремой о непрерывной зависимости решения от начальных значений.
Определение. Решение 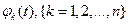 системы (1) называется устойчивым по Ляпунову, если для любого
системы (1) называется устойчивым по Ляпунову, если для любого 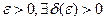 такое, что для любого
такое, что для любого 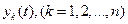 той же системы, начальные значения которого удовлетворяют неравенствам
той же системы, начальные значения которого удовлетворяют неравенствам 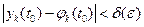 , (k = 1,2,...,n) (2).
, (k = 1,2,...,n) (2).
Для всех 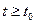 справедливы неравенства
справедливы неравенства 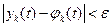 , (k = 1,2,...,n) (3), т.е. близкие по начальным значениям решения остаются близкими для всех
, (k = 1,2,...,n) (3), т.е. близкие по начальным значениям решения остаются близкими для всех 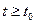 (можно писать
(можно писать 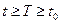 ).
).
Если при сколь угодно малом 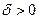 хотя бы для одного решения
хотя бы для одного решения 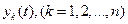 неравенство (3) не выполняется, то решение
неравенство (3) не выполняется, то решение 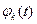 называется неустойчивым.
называется неустойчивым.
Если решение 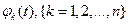 не только устойчиво, но, кроме этого, удовлетворяет условию
не только устойчиво, но, кроме этого, удовлетворяет условию 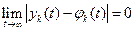 (4), это решение
(4), это решение 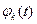 называется асимптотически устойчивым.
называется асимптотически устойчивым.
Пример. Исследовать на устойчивость решение уравнения 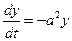 при условии
при условии 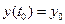 ,
, 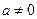
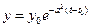 - асимптотически устойчиво, так как
- асимптотически устойчиво, так как 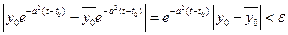 если
если 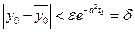 и
и 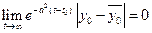 .
.
Сделаем замену в системе (1): 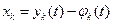 (5), (k = 1,2,...,n).
(5), (k = 1,2,...,n).
Тогда система (1) будет иметь вид: 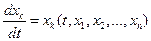 (6), и новыми неизвестными функциями
(6), и новыми неизвестными функциями 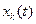 являются отклонения
являются отклонения 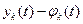 прежних неизвестных функций от
прежних неизвестных функций от 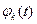 , определяющих устойчивость решения.
, определяющих устойчивость решения.
Тогда исследовать на устойчивость нужно будет тривиальное решение 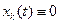 , (k = 1,2,...,n).
, (k = 1,2,...,n).
Сформулируем определение устойчивости для точки покоя: 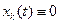 , (k = 1,2,...,n). Эта точка покоя системы (6) устойчива в смысле Ляпунова, если
, (k = 1,2,...,n). Эта точка покоя системы (6) устойчива в смысле Ляпунова, если 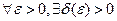 , что из неравенства
, что из неравенства 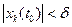 , (k = 1,2,...,n) следует
, (k = 1,2,...,n) следует 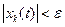 , (k = 1,2,...,n) при
, (k = 1,2,...,n) при 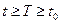 .
.
 2014-02-10
2014-02-10 462
462








