Рассмотрим линейную систему с постоянными коэффициентами
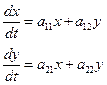 (1) и исследуем расположение траекторий в окрестности точки покоя x = 0, y = 0.
(1) и исследуем расположение траекторий в окрестности точки покоя x = 0, y = 0.
Пусть 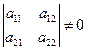 (2) тогда
(2) тогда 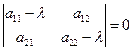 (3).
(3).
Тем самым мы предполагаем, что корни характеристического уравнения (3) отличны
от нуля.
Ι. Характеристическое уравнение имеет действительные и различные корни.
1) 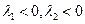 . Общее решение имеет вид
. Общее решение имеет вид 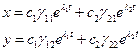 (4).
(4).
Тогда точка х = 0, у = 0 асимптотически устойчива, так как все точки, находящиеся в момент t = t0 в любой 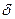 -окрестности начала координат (при
-окрестности начала координат (при 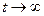 ) стремятся к началу координат.
) стремятся к началу координат.
Такая точка покоя называется устойчивым узлом.
2) 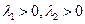 . Точка покоя неустойчива, так как движущаяся по траектории
. Точка покоя неустойчива, так как движущаяся по траектории 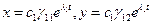 точка с возрастанием t покидает
точка с возрастанием t покидает -окрестность начала координат. Можно отметить, что есть движения, приближающиеся к началу координат:
-окрестность начала координат. Можно отметить, что есть движения, приближающиеся к началу координат: 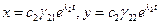 .
.
ΙΙ. Корни характеристического уравнения (3) являются комплексными.
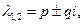
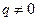 .
.
Общее решение записывается в виде:
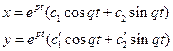 (5), где
(5), где 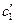 и
и 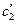 - линейные комбинации
- линейные комбинации 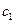 и
и 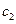 .
.
1) 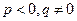 .
.
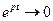 с возрастанием t, а второй множитель является ограниченным. Точки, находящиеся при
с возрастанием t, а второй множитель является ограниченным. Точки, находящиеся при 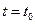 в любой
в любой 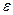 - окрестности начала координат, попадают в
- окрестности начала координат, попадают в 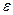 -окрестность при возрастании t. Такая точка покоя называется устойчивым фокусом.
-окрестность при возрастании t. Такая точка покоя называется устойчивым фокусом.
Фокус отличается от узла тем, что касательная к траекториям не стремится к определённому пределу при приближении точки касания к точке покоя.
2) 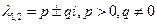 .
.
Траектории те же, но движение по ним происходит в обратном направлении. Точка покоя неустойчива. Это неустойчивый фокус.
3) 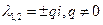 .
.
В силу периодичности решений, траектории – замкнутые кривые, содержащие внутри себя точку покоя, которая в этом случае называется центром. Центр является устойчивой точкой покоя (но асимптотически устойчивой точкой его назвать нельзя).
ΙΙΙ. Корни кратные (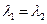 ).
).
1) 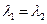 < 0.
< 0.
Общее решение имеет вид 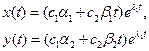 (6), причём, здесь возможна ситуация, когда
(6), причём, здесь возможна ситуация, когда 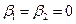 .
.
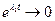 при
при 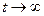 . Точки покоя называются устойчивыми узлами. Если
. Точки покоя называются устойчивыми узлами. Если 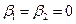 ,
,
то такой узел называется дикритическим (устойчивый).
2) 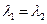 >0.
>0.
Траектории не отличаются от траектории предыдущего случая, но движение по ним происходит в обратном направлении. В этом случае точка называется неустойчивым узлом.
Рассмотрим случай, когда 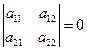 .
.
Тогда характеристическое уравнение (3) имеет нулевой корень 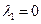 . Предположим, что
. Предположим, что 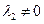 . Тогда общее решение имеет вид:
. Тогда общее решение имеет вид:
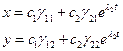 (7).
(7).
Исключая из системы (7) t, получим семейство параллельных прямых:
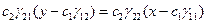 (8).
(8).
Если с2 = 0, получим однопараметрическое семейство точек покоя, расположенных на прямой 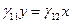 . Если
. Если 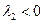 , то при
, то при 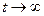 на каждой траектории точки приближаются к лежащей на этой траектории точке покоя
на каждой траектории точки приближаются к лежащей на этой траектории точке покоя 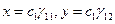 .
.
Точка покоя х = 0, у = 0 устойчива, но асимптотической устойчивости нет.
Если же 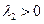 , то траектории расположены также, но движение точек на траекториях покоя осуществляется в противоположном направлении. Точка покоя х = 0, у = 0 неустойчива.
, то траектории расположены также, но движение точек на траекториях покоя осуществляется в противоположном направлении. Точка покоя х = 0, у = 0 неустойчива.
3) 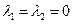 .
.
В этом случае можно выделить два подпункта:
1. Общее решение имеет вид: 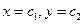 - все точки являются точками покоя, все решения устойчивы.
- все точки являются точками покоя, все решения устойчивы.
2. Общее решение имеет вид: 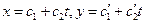 ,
, 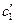 и
и 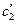 - линейные комбинации
- линейные комбинации 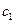 и
и 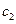 . Точка покоя х = 0, у = 0 неустойчива.
. Точка покоя х = 0, у = 0 неустойчива.
ЗАМЕЧАНИЕ. Точки покоя х = 0, у = 0 системы (1) является особой точкой уравнения 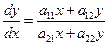 .
.
ЛЕКЦИЯ 12:
Результат об устойчивости и неустойчивости точки покоя 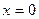 ,
, 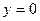 .
.
Система 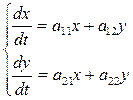
Можно распространить и на линейную систему с постоянными коэффициентами 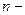 го порядка:
го порядка:
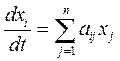 ,
, 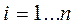
Если все действительные части корней характеристического уравнения отрицательны, то тривиальное решение это 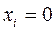 ,
, 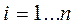 асимптотически устойчиво.
асимптотически устойчиво.
Если хоть один корень имеет действительную положительную часть, то неустойчиво.
 2014-02-10
2014-02-10 486
486








