Линейные интегральные уравнения

Интегральными уравнениями называют уравнения, в которых неизвестная функция входит под знак интеграла.

Основные классы линейных интегральных уравнений:

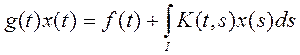(1)

(1) – общий вид, неизвестная функция входит линейно.

1) 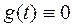, 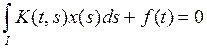– интегральное уравнение первого рода.

2) 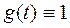, 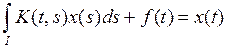– интегральное уравнение второго рода.

3) 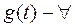функция, интегральное уравнение (1) третьего рода.

Функция 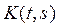, 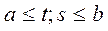называется ядром интегрального уравнения.

Если 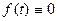, то интегральное уравнение называется однородным.

Ядро 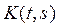и функция 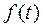– непрерывны, первая на 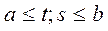, вторая на .

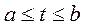Уравнение 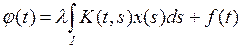(2) называется уравнением Фредгольма 2-ого рода, причём это семейство уравнений, зависящих от числового параметра .

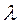Уравнением Фредгольма 1-ого рода имеет вид: 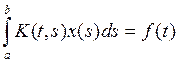(3)

Линейным интегральным уравнением Вольтера 2-ого рода называется уравнение: 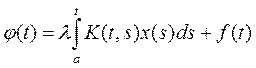, 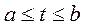(4)

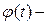неизвестная функция.

Уравнением Вольтера 1-ого рода называется уравнение: 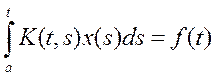(5)

Уравнение Вольтера можно рассматривать частный случай уравнение Фредгольма.

Ядро 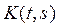определено при .

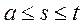Доопределяем по при 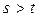следующим образом , .

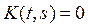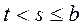Тогда уравнение (4) можно рассматривать, как частный случай уравнения Фредгольма с ядром 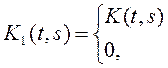, для

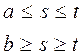
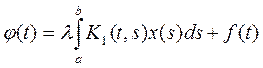(6)

Интегральные уравнения в общем виде в квадратурах не решается.