1) 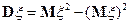
2) 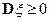
3) 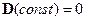
4) 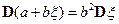
5) 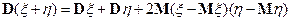 .
.
Все свойства очевидно следуют из определения.
Обозначим
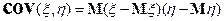
и назовем ковариацией.
6) Для независимых  и
и 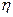
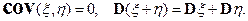
Обозначим
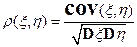
коэффициент корреляции при 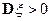 и
и 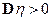
7) 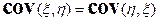 ,
, 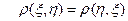
8) 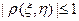
9) если 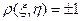 , то
, то  и
и 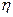 – линейно зависимы,
– линейно зависимы, 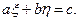
Найдем оценку 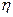 в виде
в виде 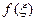 . Пусть
. Пусть 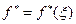 – оптимальная в среднеквадратическом смысле оценка, т.е.
– оптимальная в среднеквадратическом смысле оценка, т.е.
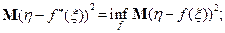
Найдем 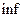 в классе линейных функций
в классе линейных функций
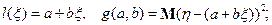
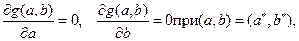
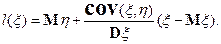
Рассмотрим схему Бернулли 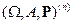 с
с 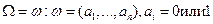 ,
, 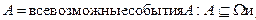 ,
,
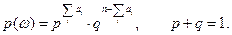
Определим случайные величины 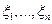 с
с 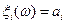 ,
, 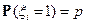 ;
; 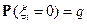 ;
; 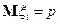 ;
; 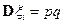 . Непосредственно проверяется, что
. Непосредственно проверяется, что 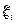 независимы в совокупности. Положим
независимы в совокупности. Положим 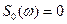 и
и 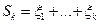 ;
; 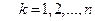 . Тогда
. Тогда
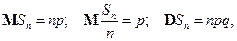
т.е. среднее значение частоты появления успеха 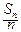 совпадает с вероятностью успеха
совпадает с вероятностью успеха 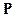 . А вот насколько числа
. А вот насколько числа 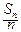 близки
близки 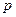 ?
?
Для ответа воспользуемся неравенством Чебышева.
Теорема. Пусть 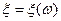 – неотрицательная простая случайная величина на произвольном вероятностном пространстве
– неотрицательная простая случайная величина на произвольном вероятностном пространстве 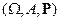 . Тогда для любого
. Тогда для любого 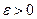
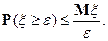
 2014-02-12
2014-02-12 318
318








