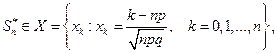
точки 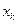 разбивают отрезок
разбивают отрезок 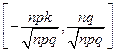 на отрезки длиной
на отрезки длиной 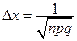 ;
;
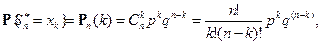
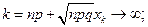
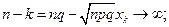
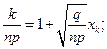
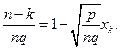
Покажем, что при 
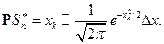
По формуле Стирлинга
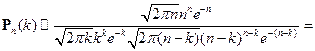
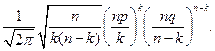
Так как
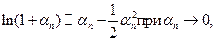
то
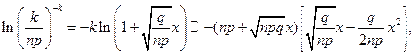
и
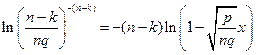
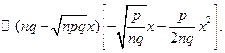
Сложим эти выражения.
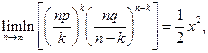
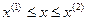 , следовательно,
, следовательно,
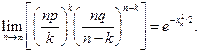

следовательно,
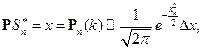
что и требовалось доказать.
Заметим, что в условиях теоремы ограничение 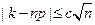 можно заменить на
можно заменить на 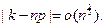
Из локальной предельной теоремы вытекает интегральная предельная теорема для схемы серий Бернулли, или так называемая теорема Муавра-Лапласа.
Теорема. В предположениях локальной теоремы, 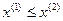 ,
,
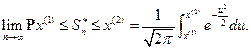
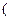 Заметим, что
Заметим, что 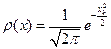 – так называемая плотность гауссовского или нормального распределения
– так называемая плотность гауссовского или нормального распределения 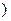 .
.
Доказательство. При 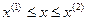 таких, что
таких, что 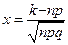 по локальной теореме
по локальной теореме
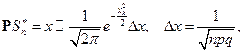

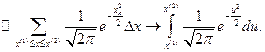
Теорема доказана.
Заметим, что из теоремы Муавра-Лапласа следует закон больших чисел, так как

и, следовательно,
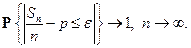
Рассмотрим схему серий Бернулли 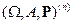 ,
, 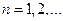 с распределением
с распределением
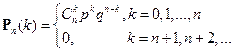
и пусть 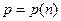 – функция
– функция 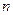 .
.
Справедлива следующая теорема Пуассона:
Теорема. Пусть 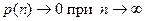 так, что
так, что  .
.
Тогда для любого 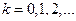
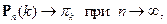
где 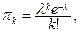
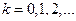 так называемое распределение Пуассона.
так называемое распределение Пуассона.
Доказательство.
|
|
|
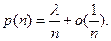
Следовательно, для любого фиксированного 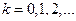
при больших 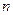
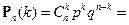
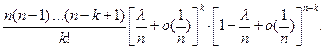
Однако
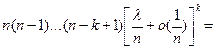
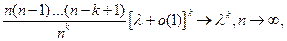
и
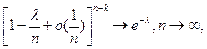
что и доказывает теорему.
Набор  образует так называемое пуассоновское распределение, так как
образует так называемое пуассоновское распределение, так как 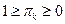 ;
; 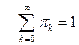 .
.
Рассмотрим понятия условных вероятностей и математических ожиданий относительно разбиений. Пусть 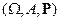 – конечное вероятностное пространство и
– конечное вероятностное пространство и  – некоторое разбиение
– некоторое разбиение 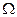 , такое что
, такое что 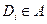 ,
, 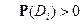 .
.
Для 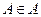 определена
определена
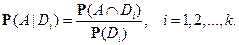
Определение. Случайная величина 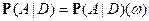 определяется как
определяется как
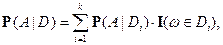
и называется условной вероятностью события 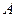 относительно разбиения
относительно разбиения 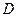 .
.
Свойства:
1) 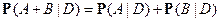 при
при 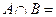
2) если 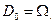 , то
, то 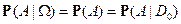
3) 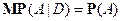 , т.е.
, т.е. 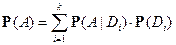 , т.е. формула полной вероятности.
, т.е. формула полной вероятности.
Пусть 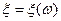 – случайная величина со значениями в
– случайная величина со значениями в 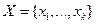 .
.
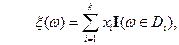
где 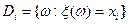 ; разбиение
; разбиение 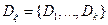 – порождено случайной величиной
– порождено случайной величиной  .
.
Определение. 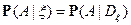 – условная вероятность события
– условная вероятность события 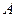 при условии случайной величины
при условии случайной величины  .
.
Заметим, что 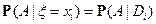 .
.
Аналогично, если 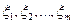 – случайные величины,
– случайные величины, 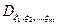 – разбиение порожденное
– разбиение порожденное 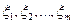 с атомами
с атомами
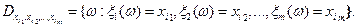
Обозначим 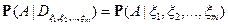 .
.
Определение. 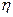 измерима относительно
измерима относительно 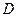
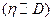 , если
, если 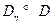
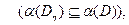 т.е. если
т.е. если
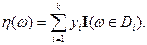
Теорема. Пусть  – простая случайная величина,
– простая случайная величина, 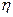 – простая случайная величина и
– простая случайная величина и 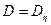 . Пусть
. Пусть 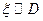 .
.
Тогда 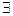 функция
функция 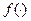 , такая, что
, такая, что 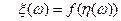 .
.
 2014-02-12
2014-02-12 431
431








