2014-02-12
2258
Из классического выражения для кинетической энергии на основании третьего постулата следует выражение для оператора кинетической энергии
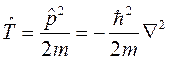(2.8)
Оператор координаты.
Действие оператора координаты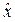 
на функцию определяется как умножение функции на саму координату, то есть
,
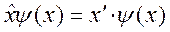где х’ - числовое значение координаты. Таким образом, оператор координаты имеет непрерывный спектр собственных значений. Определим его собственные функции. Пусть собственной функции y0 соответствует конкретное собственное значение х 0. Тогда можно записать:
,
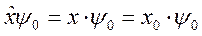где х – переменная. Это равенство при х ≠ х 0 выполняется только тогда, когда y0=0, а при х = х 0 функция y0 может иметь любое значение. Как собственные функции оператора, имеющего непрерывный спектр, они нормированы на δ - функцию, поэтому может быть только y0=∞. А это значит, что y0 удовлетворяет определению δ - функции. Таким образом, собственными функциями оператора координаты являются просто δ - функции
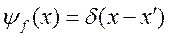, (2.9)
Плотность вероятности того, что частица, описываемая волновой функцией ψ (х) имеет координату х ¢, есть
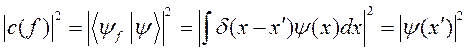
Средние значения.
Поскольку поведение квантовых частиц случайно, то любой физический процесс, описываемый измеряемой величиной F и соответствующим оператором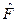 
, имеет вероятностный исход, который характеризуется средним значением.
Среднее значение непрерывной случайной функции F (x) от случайной величины х на интервале [ a,b ] по определению есть
,
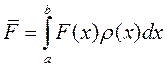где ρ (х) – функция распределения случайной величины х, дающая вероятность нахождения, в нашем случае, частицы в точке х. Тогда на основании 1-го постулата квантовой механики
.
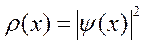Тогда в общем случае конфигурационного пространства
,
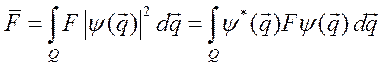или, переходя к квантовым обозначениям,
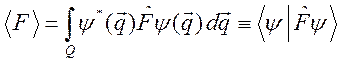. (2.10)
Для волновых функций, нормированных на единицу, получим
,
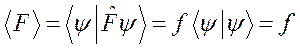то есть среднее (измеряемое) значение физической величины равно собственному значению оператора этой величины.
Среднее значение координаты частицы, описываемой волновой функцией y, нормированной на 1, есть
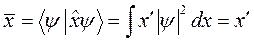
Вычислим среднее значение импульса свободно движущейся частицы. Волновая функция такой частицы есть «волновой пакет»
.
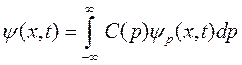Тогда
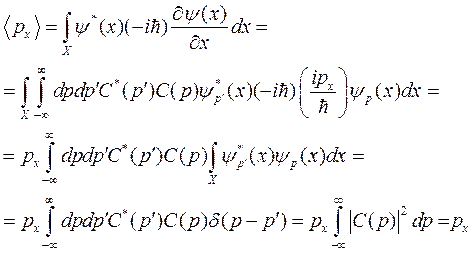
Важно отметить, что поскольку нормировка (1.9) и средние значения физических величин (2.10) включают произведение величин y и y*, то волновая функция определена с точностью до произвольного множителя вида ei a.
