Лекция №5. Примеры решения уравнения Шредингера в простейших случаях

Примеры решения уравнения Шредингера в простейших случаях.

1. Потенциальная яма с бесконечно высокими стенками (движение внутри сегмента [0, а ]).

В этом случае потенциальная функция имеет вид:

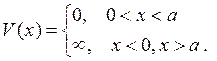
Уравнение для координатной части волновой функции перепишем в виде:

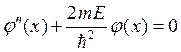. (8.1)

Ищем решение в виде 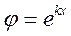, где k - волновое число. Тогда из последнего уравнения имеем

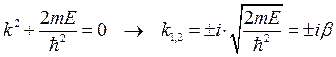(8.2)

и общее решение запишем в виде:

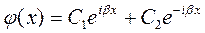. (8.3)

Поскольку вероятность частице находиться на краях ямы, где потенциальная энергия бесконечна, может быть только равна нулю, то граничные условия при х =0 и х = а имеют вид:

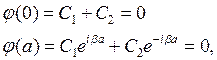
откуда имеем

С ₂ = – С ₁,

,

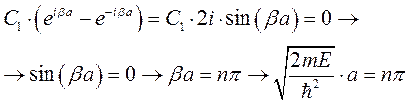и получаем дискретный спектр энергий

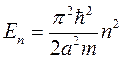. (8.4)

Таким образом, для n -го собственного значения энергии функция j имеет вид:

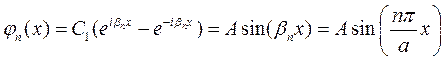, (8.5)

где амплитуда А определяется из условия нормировки:

.

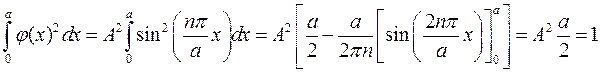Таким образом, полная волновая функция частицы в потенциальной яме с бесконечно высокими стенками есть

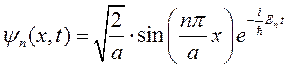. (8.6)

В природе такая ситуация реализуется, например, для кварков, которые образуют, в частности, протоны и нейтроны. Их неотъемлемым свойством является невозможность их существования в свободном состоянии (конфайнмент – «пленение» кварков), что объясняется наличием в нуклоне потенциальной ямы с бесконечно высокими стенками.

2. Потенциальная яма со стенками конечной высоты.

По-прежнему в области 0< x < a (область II) V =0, волновая функция частицы (точнее, ее координатная часть) определяется уравнением Шредингера (8.1), а общее решение имеет вид (8.3). Но, в отличие от предыдущего примера, граничные условия на краях потенциальной ямы не нулевые, а должны отражать непрерывность и непрерывную дифференцируемость волновой функции при переходе из потенциальной ямы (область II) в область I (х <0) или область III (х > а) (рис. 5.1).

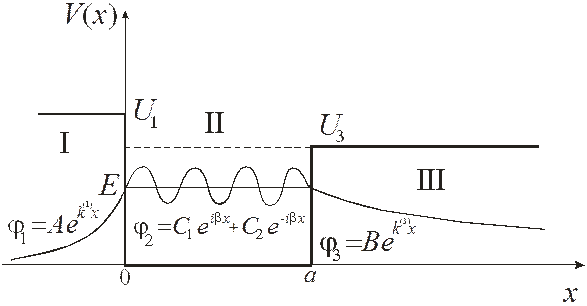
Рис.5.1. Потенциальная яма со стенками конечной высоты

Уравнение Шредингера для областей I и III имеет вид

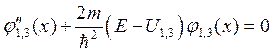, (8.7)

тогда для волновых чисел вместо (8.2) имеем

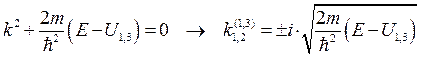(8.8)

Из последнего выражения видно, что для энергии частицы Е < U _1,3 волновые числа действительны и решения при удалении от потенциальной ямы имеют экспоненциально нарастающий или экспоненциально убывающий вид. Физический смысл имеют только экспоненциально убывающие решения, поэтому для х <0 (область I)

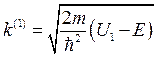и 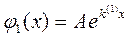, (8.9)

для х > a (область III)

и 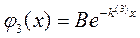, (8.10)

а внутри потенциальной ямы

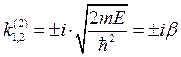и 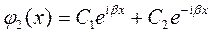(8.11)

На границах потенциальной ямы должны выполняться условия:

при х =0

(8.12а)

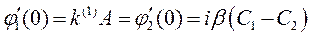, (8.12б)

при х = а

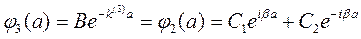(8.12в)

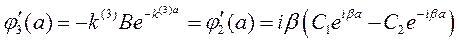(8.12г)

Соотношения (8.12) образуют систему 4 однородных алгебраических уравнений относительно 4 неизвестных амплитуд А, В, С ₁, С ₂. Для нетривиального решения этой системы необходимо и достаточно, чтобы ее определитель был равен нулю:

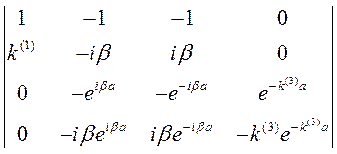=0. (8.13)

Соотношение (8.13) дает трансцендентное уравнение относительно энергии, действительные корни которого (рис. 5.2) определяют уровни энергии Е_n в потенциальной яме при условии, что Е <min(U ₁, U ₃). При другом соотношении энергии и высоты стенок «ямы» (краевых потенциальных барьеров) действительных корней нет, могут быть только комплексные, что соответствует непрерывному спектру. Таким образом, при сообщении частице энергии, превышающей высоту «ямы», она становится свободной.

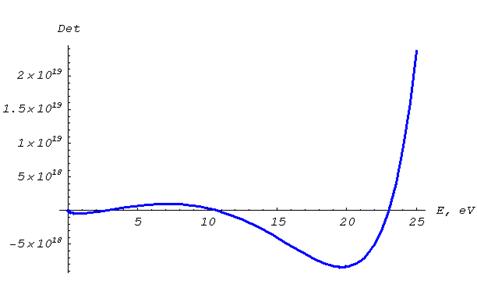
Рис. 5.2. Вид трансцендентной функции Re[Det(8.13)] и ее корни.

3. Прохождение частицы через потенциальный барьер (туннельный эффект)

В физике микромира существуют физические процессы, не имеющие аналога в макромире. Одним из таких процессов является туннельный эффект, который лежит в основе механизма работы большого числа современных технических устройств: от полупроводниковых приборов до управляемого термоядерного реактора.

Туннельный эффект – чисто квантовый эффект, заключающийся в проникновении частицы сквозь потенциальный барьер при ее собственной энергии меньшей, чем высота барьера. Рассмотрим свободный электрон с энергией Е ₀, движущийся в положительном направлении оси х к потенциальному барьеру высотой U ₂ (рис. 5.3).

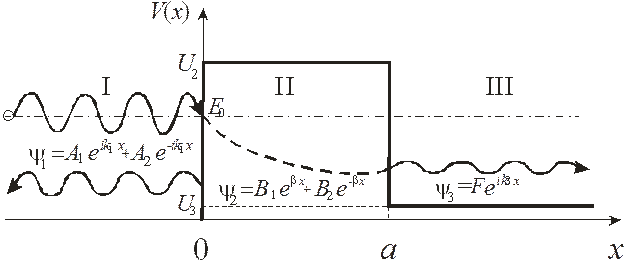
Рис. 5.3. К расчёту туннельного эффекта

Волновую функцию электрона в областях I, II и III определим из уравнения Шредингера

,

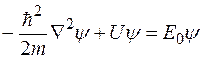где потенциальная энергия U в областях I, II и III принимает соответственно значения 0, U₂ и U₃. Общие решения для этих областей (по аналогии с предыдущим примером) будут иметь вид

,

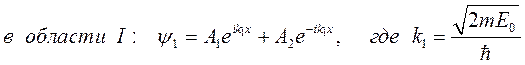то есть в этой области одновременно существуют падающая волна (с амплитудой А ₁) и отраженная от потенциального барьера волна (с амплитудой А ₂);

,

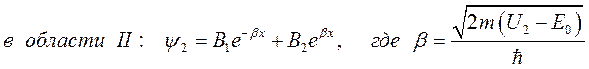то есть в этой области прошедшая волна (с амплитудой В ₁) и отраженная от правого края барьера волна (с амплитудой В ₂) являются нераспространяющимися (затухающими) волнами и, складываясь, они определяют немонотонное распределение вероятности нахождения электрона в области потенциального барьера;

,

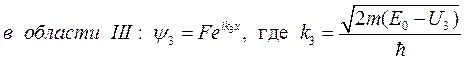то есть в этой области существует только распространяющаяся волна (имеющая амплитуду F), уходящая от барьера.

В точках х =0 и х=а должна выполняться непрерывность волновых функций и их производных, откуда следуют четыре неоднородных алгебраических уравнения для четырех отношений амплитуд А₂ /А₁, В₁ /А₁ , В₂ /А₁ , F/А₁ . Решая эту систему, получим аналитические выражения для искомых величин, которые, однако, из-за их громоздкости не приводятся.

Найденные величины определяют коэффициент прозрачности барьера:

и коэффициент отражения от барьера:

.

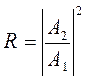Очевидно, должно выполняться соотношение:

R + D =1.

Ввиду важности коэффициента прозрачности приведем его выражение для частного случая U ₃=0 (при этом и k ₃ = k ₁)

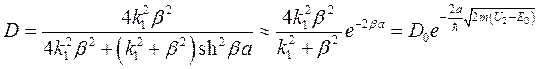(8.14)

Приближенное равенство соответствует обычно выполняющемуся соотношению βа >1 или а>l _ДБ. Из (8.14) видно, что туннельный эффект сильно зависит от ширины барьера и разности энергий частицы и барьера. Так, например, для электрона в зоне проводимости (Е ₀ ~1 эВ) при ширине барьера a»1 нм (10 ангстрем) и высоте барьера U₂-Е ₀»1 эВ коэффициент прозрачности D»10^-6

а

. Это означает, что туннельные токи имеют, как правило, очень малые величины.

В реальных задачах потенциальный барьер имеет форму более сложную, чем прямоугольник. В этом случае можно разбить барьер на множество малых прямоугольных барьеров и, используя формулу (8.14), вычислить коэффициент прозрачности с помощью интегрирования:

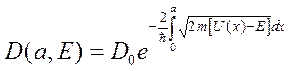(8.15)