2014-02-12
697
Пусть проводится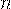 
независимых испытаний, причем 
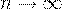, вероятность появления некоторого события
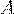в отдельном испытании постоянна и равна 
, 
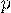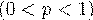, то есть 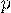и , и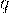 
заметно отличны от нуля, тогда вероятность того, что событие 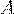появится 
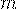раз в 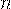испытаниях вычисляется по
локальной формуле Лапласа:
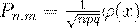(29)
где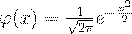 
(30)
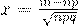(31)
Формулу (29) чаще используют пр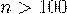и 
и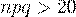 
.
Для упрощения расчетов, связанных с применением формулы (29), составлена таблица значений локальной
функции Лапласа, которая имеется в справочном модуле. Пользуясь этой таблицей, нужно учитывать
следующие свойства функции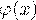 
:
1. 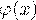- четная функция, то есть 
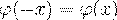, поэтому в таблице приведены значения
только для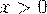 
;
2. 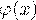монотонно убывает при ;
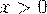3. если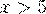 
, то можно считать, что 
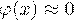, поэтому таблица приведена только до 
.
Пример 33. Вероятность появления события 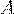в одном из 400 независимых испытаний равна 0,2.
Найти вероятность того, что данное событие появится 80 раз.
Решение. По условию,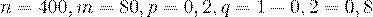 
. Воспользуемся локальной формулой Лапласа.
Сначала вычислим значение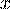 
: 
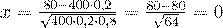, по таблице находим 
.
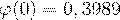Искомая вероятность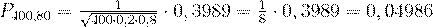 
.
Вопрос. Вероятность поражения мишени при одном выстреле равна 0,75. Тогда вероятность того, что при
100 выстрелах мишень будет поражена 70 раз равна(округлить до тысячных).
0,049
0,047
0,04
0,048
