2014-02-12
1294
Задание – На примере конкретного туроператора
По принадлежности туристского продукта.
Туроператор всегда имеет запас туристского продукта для продажи, а турагент запрашивает определенный продукт (услугу) только тогда, когда клиент выражает покупательский интерес.
1. Общая характеристика, дата создания, сайт, награды;
2. Основные направления деятельности;
3. Страны и курорты, которые предлагает ТО из Н.Новгорода и Москвы
4. Даты перелета и самолеты, на которых осуществляется перевозка пассажиров;
5. Полезная информация на сайте
Пусть производится несколько испытаний, в результате которых может появиться некоторое событие
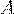с определенной вероятностью.
Определение 27. Если вероятность события 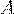в каждом испытании не зависит от исходов других испытаний,
то такие испытания называются независимыми относительно события .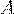
Предположим, что в одинаковых условиях проводятся n независимых испытаний, в каждом из которых
вероятность появления события 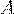равна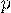 
. Нужно найти вероятность того, в этих n испытаниях событие
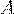произойдет m раз. Непосредственное применение теорем сложения и умножения вероятностей для
поставленной задачи с увеличением числа испытаний приводит к очень громоздким вычислениям. Необходимо
применение других способов.
Обозначим события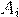 
={событие 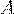произошло в 
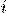-ом испытании}, где i=1,2,...,n.
, тогда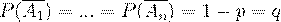 
.
Событие 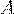в n независимых испытаниях может появится ровно m раз в разных комбинациях, например,
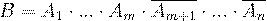и так далее, таких
комбинаций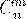 
. По условию, испытания независимые, поэтому события, входящие в комбинации, тоже
независимые, следовательно,
.
Так как все комбинации, подобные комбинации 
, являются несовместными событиями и не важно, в какой
последовательности появляется событие и в какой событие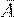 
, то по теореме сложения
вероятностей для несовместных событий:
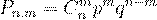(23)
Данная формула называется формулой Бернулли.
Она имеет важное значение в теории вероятностей, так как она связана с повторением испытаний в одинаковых
условиях, в которых как раз и проявляются законы теории вероятностей.
Так как события, состоящие в различном числе появлений события 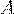в серии из n испытаний, несовместны и
образуют полную группу, то
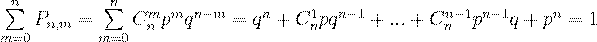(24)
Пример 30. Вероятность изготовления на станке стандартной детали равна 0,9. Найти вероятность того, что
из 6 наудачу взятых деталей 4 будут стандартными.
Решение. Так как извлечение деталей - это независимые испытания, то вероятность того, что из 6 извлеченных
деталей 4 стандартные, надо вычислять по формуле (23):
.
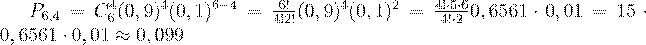Определение 28. Наивероятнейшим числом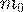 
появления события 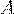в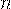 
независимых испытаниях
называется число, для которого вероятность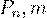 
не меньше вероятностей каждого из остальных
возможных исходов испытаний.
Данное число 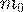удовлетворяет следующим условиям:
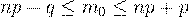(25)
Длина интервала, определяемого этими неравенствами равна: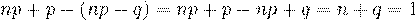 
.
Если границы этого интервала дробные числа, то для 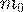получаем одно значение:
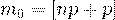(26)
где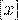 
- целая часть числа 
.
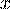Если границы интервала - целые числа, то для 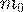получаем два значения (концы интервала):
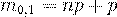(27)
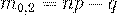
Пример 31. Вероятность поражения самолета равна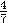 
. Найти наиболее вероятное число пораженных
самолетов в группе из 13 бомбардировщиков, если самолеты поражаются независимо друг от друга.
Решение. Число испытаний - это число самолетов,так как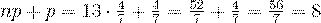 
, то для 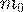получаем два значения: 
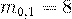и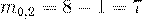 
.
Вопрос. При данном технологическом процессе 85% продукции - высшего сорта.
Наивероятнейшее число изделий высшего сорта в партии из 150 изделий равно.
Формула Пуассона
В приложениях часто приходится вычислять вероятности различных событий, связанных с числом успехов
в 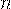испытаниях схемы Бернулли при больших значениях 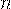. В этом случае по формуле Бернулли
вычисления становятся затруднительными. Затруднения при вычислениях возникают и в случае малых значени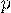й и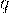 
. Если число независимых испытаний велико, то есть 
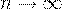, а вероятность появления некоторого
события 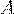в отдельном испытании мала, то есть 
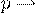, но так, что 
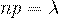, то вероятность того, что
в 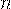независимых испытаниях событие 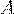появится 
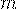раз вычисляется по формуле Пуассона:
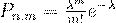(28)
Пример32. Телефонная станция обслуживает 400 абонентов. Для каждого абонента вероятность того,
что в течение часа он позвонит на станцию, равна 0,01. Найти вероятность того, что в течение часа 5
абонентов позвонят на станцию.
Решение. Согласно условию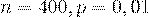 
, то есть число испытаний велико, а вероятность появления
события(звонок абонента) в отдельном испытании мала, тогда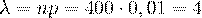 
.
В соответствии с формулой (28) находим:
.
Если мало , то есть вероятность непоявления события в отдельном испытании, то формулу Пуассона
можно использовать для вычисления вероятности того, что в 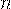независимых испытаниях событие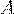
не появилось 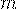раз.
Вопрос. Если число независимых испытаний равно 10, то вероятность того, что событие произошло 4 раза,
надо вычислять по формуле Пуассона.
неверно
верно
