Интегральная формула Лапласа

Пусть производится 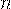независимых испытаний, в каждом из которых вероятность появления события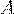
постоянна и равна 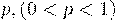. Вероятность того, что в этих испытаниях событие 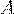появится от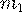
до 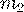раз, вычисляется по интегральной формуле Лапласа:

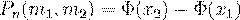(32)

где 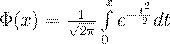(33)

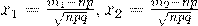(34)

При решении задач, требующих применения формулы (32), пользуются таблицей для функции ,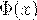
эта функция называется функцией Лапласа. Таблица значений функции Лапласа приведена в справочном
модуле. При использовании таблицы надо учитывать следующие свойства данной функции:
1. функция Лапласа нечетная, то есть , поэтому в таблице приведены значения только
для ;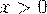
2. функция Лапласа монотонно возрастает при ;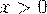
3. при 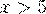можно считать, что 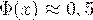, поэтому таблица приведена только до .

Пример 34. Вероятность того, что деталь не прошла проверку, равна 0,2. Найти вероятность того, что
среди 400 случайно отобранных деталей, не прошедших проверку окажется от 70 до 100 деталей.
Решение. По условию, .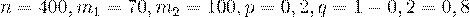
Воспользуемся интегральной формулой Лапласа, сначала вычислим значения :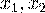

,

.

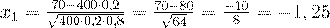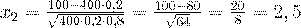По таблице находим: .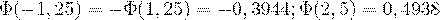

Тогда искомая вероятность .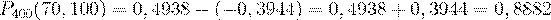

Вопрос. Если , то .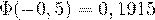

верно

неверно