Рассмотрим опыт, состоящий в бросании случайным образом точки на отрезок [ a; b ], предполагая, что попадания в любую точку равновозможны. Пространство элементарных событий W в этом опыте – все точки отрезка [ a; b ]. Поскольку множество элементарных событий несчетно (бесконечно) и все они равновозможны, то для "wÎW P (w)=0. Так, что классическая схема неприменима. В этом случае положим, что вероятность события A – «Попадание брошенной точки на отрезок [ c; d ] Ì [ a; b ]» – пропорциональна длине отрезка [ c; d ], т.е. P (A) = k ·(d - c), где d - c – длина отрезка. Коэффициент k находится из условия нормировки: P (W) = k ·(a - b) =1 Þ k = 1/(a - b) и P (A) = (d - c)/(a - b).
Пример 2.8. Абонент ждет телефонного вызова в течение одного часа. Какова вероятность, что вызов произойдет в последние 20 минут этого часа?
Решение. Пусть событие A состоит в том, что вызов произошел в последние 20 минут. Изобразим пространство элементарных событий в виде отрезка длины 60. Тогда элементарные события, благоприятные A, заключены в последнюю треть отрезка, следовательно, P (A) = 1/3. Ответ: 1/3.
Естественно, что вместо отрезка можно говорить о плоской фигуре, определив вероятность как отношение P (A) = S (A)/ S (W), где S (A) и S (W) – площади соответствующих фигур.
Пример 2.9. Два лица X и Y условились встретиться в определенном месте между 12 часами и часом, при этом пришедший первым ждет другого в течение 20 минут, после чего уходит. Чему равна вероятность встречи лиц X и Y, если приход каждого из них в течение указанного часа может произойти случайно, и моменты прихода независимы?
Решение. Обозначим момент прихода лица X через x, а лица Y через y. Для того, чтобы встреча произошла, необходимо и достаточно выполнение неравенства | x – y | £20. На координатной плоскости множество точек, удовлетворяющие этому неравенству, изобразятся в виде полосы (рис. 2.2а), все возможные исходы – точками квадрата со стороной 60 (минут), а благоприятствующие встрече – расположатся в заштрихованной области (рис. 2.2б). Следовательно, искомая вероятность равна отношению площади заштрихованной фигуры к площади всего квадрата, т.е. равна (602 – 402)/602 = 5/9.
Ответ: 5/9.
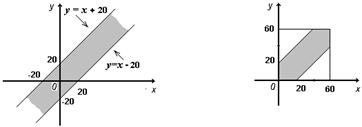 | |
| a) | б) |
| Рис.2.2 |
 2014-02-12
2014-02-12 2608
2608








