Угол между прямыми

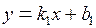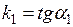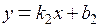Рассмотрим на плоскости две прямые ₁ и ₂ (рис. 2.4). Пусть уравнение прямой ₁ имеет вид , где , а уравнение прямой ₂ – вид , где 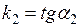. Под углом j между двумя прямыми будем понимать наименьший угол, отсчитываемый против часовой стрелки, на который вторая прямая повернута относительно первой ().

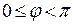y ₂ j ₁

a₁ a₂

0 x

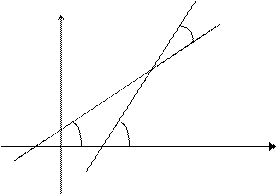
Рис. 2.4

Если a₁ и a₂ – углы наклона прямых ₁ и ₂ к оси Ох, соответственно, то j = a₂ –a₁. Отсюда

.

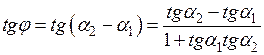Так как 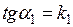, , 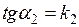то

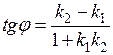. (2.10)

Формула (2.10) дает выражение тангенса угла между двумя прямыми через угловые коэффициенты этих прямых.

Выведем условия параллельности и перпендикулярности двух прямых.

Если прямые ₁ и ₂ параллельны, то j = 0, tg j = 0 и из формулы (2.10) имеем: 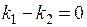, откуда

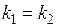. (2.11)

Обратно, если выполнено условие (2.11), то, учитывая, что a₁ и a₂ заключаются в пределах от 0 до p, получаем a₁ = a₂, и, следовательно, рассматриваемые прямые или параллельны, или совпадают (параллельность в широком смысле).

Таким образом, прямые на плоскости параллельны в широком смысле тогда и только тогда, когда их угловые коэффициенты равны между собой.

Если прямые ₁ и ₂ перпендикулярны, то j = 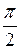и, следовательно,

;

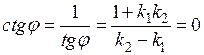отсюда 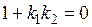и

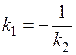. (2.12)

Аналогично можно показать, что если выполнено условие (2.12), то прямые ₁ и ₂ перпендикулярны.

Таким образом, две прямые на плоскости перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратны по величине и противоположны по знаку (для прямых, параллельных осям Ох и Оу, условно полагают 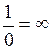и ).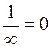

Пусть теперь уравнения прямых заданы в общем виде:

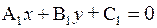и .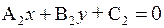

Предположим, что В₁≠0 и В₂≠0. Тогда угловые коэффициенты
этих прямых равны 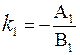и 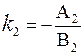, соответственно.
Из формул (2.11) и (2.12) получим условие параллельности прямых:

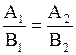; (2.13)

условие перпендикулярности прямых:

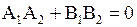. (2.14)

Формула (2.13) выражает условие коллинеарности нормальных векторов прямых, а формула (2.14) – условие ортогональности этих векторов.