Взаимное расположение прямых на плоскости

Пусть на плоскости заданы две прямые ₁ и ₂. Прямая ₁ имеет уравнение

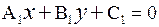, (2.15)

а прямая ₂ – уравнение

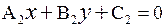. (2.16)

Выясним, как по заданным уравнениям прямых ₁ и ₂ можно судить
об их взаимном расположении.

Возможны три случая:

1. Прямые ₁ и ₂ совпадают. Отсюда следует, что их нормальные векторы n ₁ = (А₁,В₁) и n ₂ = (А₂,В₂) коллинеарны. Тогда найдется такое число k, что n ₂ = k n ₁, т.е. А₂ = kА₁, В₂ = kВ₁. Любая точка прямой ₁ (или ₂) удовлетворяет каждому из уравнений (2.15) и (2.16), а значит, и уравнению

,

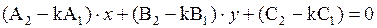или

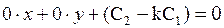, (2.17)

которое получится, если из обеих частей уравнения (2.16) вычесть соответствующие части уравнения (2.15), умноженные на k. Но уравнение (2.17) имеет решение только в том случае, когда его свободный член равен нулю, т.е. С₂=kС₁.

Итак, условием совпадения прямых ₁ и ₂ является существование такого числа k, что А₂ = kА₁, В₂ = kВ₁, С₂ = kС₁, т.е. условие пропорциональности коэффициентов уравнений.

2. Прямые ₁ и ₂ не совпадают и параллельны. Как и в первом случае, отсюда следует, что их нормальные векторы коллинеарны, т.е. А₂ = kА₁, В₂ = kВ₁. Но теперь должно быть С₂ ¹ kС₁, иначе прямые ₁ и ₂ будут совпадать.

Итак, условием того, что прямые ₁ и ₂ параллельны, но не совпадают, является существование такого числа k, что

А₂ = kА₁, В₂ = kВ₁, С₂ ¹ kС₁.

3. Прямые ₁ и ₂ не параллельны, т.е. пересекаются в одной точке.
В этом случае их нормальные векторы n ₁ и n ₂ не коллинеарны. И обратно: если n ₁ и n ₂ не коллинеарны, то сами прямые ₁ и ₂ не параллельны.

Итак, условием того, что прямые ₁ и ₂ не параллельны и не совпадают, является неколлинеарность их нормальных векторов n ₁ и n ₂, т.е. .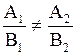

Если прямые ₁ и ₂ не параллельны, их точку пересечения можно найти, решая систему уравнений (2.15), (2.16).

Пример. Исследовать взаимное расположение пар прямых. В случае пересечения прямых найти координаты точки пересечения:

а) 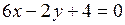, 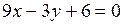; б) , ;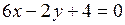

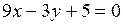в) , .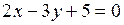

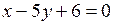○ а) Прямые 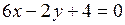и 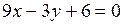совпадают,
так как 6:9 = (–2):(–3) = 4:6.

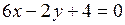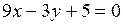б) Прямые и параллельны, но не совпадают, так как 6:9 = (–2):(–3) ¹ 4:5.

в) Прямые 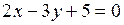и 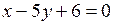не параллельны, так
как нормальные векторы n ₁ = (2,–3) и n ₂ = (1,–5) этих прямых не коллинеарны. Точку пересечения прямых находим в результате решения системы

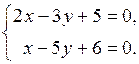
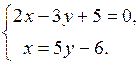
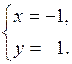
Итак, прямые пересекаются в точке (–1,1). ●