Уравнение прямой линии на плоскости

На плоскости выберем декартову прямоугольную систему координат.

Положение прямой на плоскости можно определить различными способами. Рассмотрим некоторые из них.

На плоскости прямую линию можно определить, если задать:

– одну из точек М₀ прямой и ненулевой вектор n, которому должна быть перпендикулярна прямая (нормальный вектор прямой).

– одну из точек М₀ прямой и ненулевой вектор a, которому должна быть параллельна прямая (направляющий вектор прямой).

– две точки М₁ и М₂, через которые должна проходить прямая.

– одну из точек М₀ прямой и угол j, который прямая должна составлять с положительным направлением оси Ох.

Выведем уравнение прямой для каждого из этих случаев.

Выведем уравнение прямой , проходящей через данную точку М₀(х₀,у₀) перпендикулярно ненулевому вектору n = (А,В). Любой ненулевой вектор, перпендикулярный данной прямой, называется нормальным вектором этой прямой. Вектор n = (А,В) – нормальный вектор прямой, ненулевой, т.е. .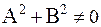

Возьмем произвольную точку М(х,у) и рассмотрим вектор
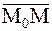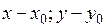= (). Точка М(х,у) тогда и только тогда будет принадлежать прямой , когда вектор 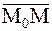перпендикулярен
вектору n, т.е. тогда и только тогда, когда скалярное произведение этих векторов равно нулю:

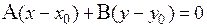. (2.3)

Итак, точка М(х,у) принадлежит прямой тогда и только тогда, когда ее координаты удовлетворяют условию (2.3). Следовательно, это условие и определяет уравнение прямой .

Таким образом, уравнение прямой, проходящей через точку М₀(х ₀, у ₀) перпендикулярно вектору n =(А,В), имеет вид (2.3).

Пример. На плоскости даны три точки: А(–1; 2), В(3; 5), С(4; –2). Убедиться, что фигура АВС – треугольник, и составить уравнение высоты, проведенной из вершины А.

○ Точки А, В, С являются вершинами треугольника, если они не лежат на одной прямой. Рассмотрим векторы: 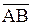=(4; 3), =(1;–7). Эти векторы неколлинеарны, значит, точки А, В, С не лежат на одной прямой и фигура АВС является треугольником. Составим уравнение высоты АD (AD^ВС). Прямая АD проходит через точку А(–1; 2).
В качестве нормального вектора прямой AD можно взять вектор
=(1;–7). Значит, уравнение высоты имеет вид 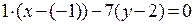. Преобразовав полученное уравнение, получим уравнение высоты АD: . ●

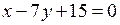Замечание. В качестве нормального вектора прямой можно взять любой другой ненулевой вектор, коллинеарный вектору n = (А,В); уравнение прямой при этом останется равносильным записанному.

□ Действительно, рассмотрим ненулевой вектор n ₁ = (А₁,В₁), коллинеарный нормальному вектору прямой n = (А,В). Векторы n ₁ и n коллинеарны, значит, линейно зависимы. Тогда существует k (k¹0) такое, что n ₁= k n, т.е. 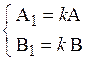. Составим уравнение прямой, проходящей через точку М₀(х ₀, у ₀) перпендикулярно вектору n ₁=(А₁,В₁): 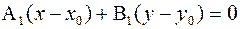, или 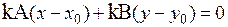. Поделив обе части уравнения на k, получим уравнение (2.3). ■