Пусть на плоскости дана точка М0(х0,у0) и прямая 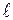 , определяемая уравнением Ах+Ву+С = 0. Требуется определить расстояние d от точки М0 до прямой
, определяемая уравнением Ах+Ву+С = 0. Требуется определить расстояние d от точки М0 до прямой  (рис. 2.5.).
(рис. 2.5.).
 y M0
y M0
n 
M1
x
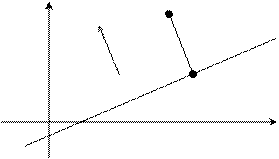
Рис. 2.5
Расстояние от точки М0 до прямой  равно длине перпендикуляра М0М1, опущенного из точки М0 на прямую
равно длине перпендикуляра М0М1, опущенного из точки М0 на прямую  , т.е. М0М1=d. Так как вектор n = (А,В) – нормальный вектор прямой
, т.е. М0М1=d. Так как вектор n = (А,В) – нормальный вектор прямой  , то векторы n и
, то векторы n и 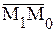 коллинеарны. Скалярное произведение этих векторов
коллинеарны. Скалярное произведение этих векторов
(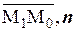 )=
)=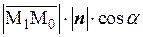 ,
,
откуда
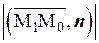 =
=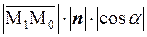
и, учитывая, что 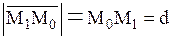 ,
, 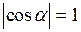 , получим
, получим
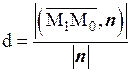 . (2.18)
. (2.18)
Вектор 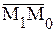 имеет координаты (х 0– х 1, у 0– у 1), вектор n = (А,В), тогда
имеет координаты (х 0– х 1, у 0– у 1), вектор n = (А,В), тогда
(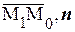 ) = А(х 0– х 1)+В(у 0– у 1) = А х 0+В у 0 –А х 1– В у 1.
) = А(х 0– х 1)+В(у 0– у 1) = А х 0+В у 0 –А х 1– В у 1.
Так как точка М1 лежит на прямой  , то ее координаты удовлетворяют уравнению этой прямой, т.е. А х 1+ В у 1+С = 0 и С = –А х 1– В у 1.
, то ее координаты удовлетворяют уравнению этой прямой, т.е. А х 1+ В у 1+С = 0 и С = –А х 1– В у 1.
Таким образом,
(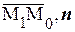 ) = А х 0+В у 0+С. (2.19)
) = А х 0+В у 0+С. (2.19)
С учетом равенства (2.19) и того, что длина вектора 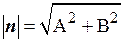 , формулу (2.18) можно записать в виде
, формулу (2.18) можно записать в виде
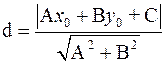 (2.20)
(2.20)
Формула (2.20) определяет расстояние от точки М0 до прямой  .
.
Пример. Даны уравнения сторон треугольника АВС: 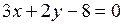 (АВ),
(АВ), 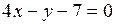 (АС),
(АС), 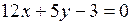 (ВС). Найти длину высоты АD, проведенной из вершины А к стороне ВС.
(ВС). Найти длину высоты АD, проведенной из вершины А к стороне ВС.
○ Длину высоты АD треугольника можно вычислить как расстояние от точки А до стороны ВС. Точка А есть точка пересечения прямых АВ и АС, значит, координаты этой точки найдем, решая систему уравнений:
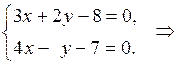 А(2;1).
А(2;1).
Расстояние от точки А до прямой ВС вычислим по формуле (2.20)
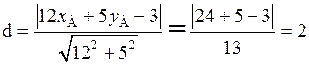 . ●
. ●
 2014-02-12
2014-02-12 844
844








