Определение. Уравнением поверхности в пространстве Охуz называется такое уравнение между переменными х, у, z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности.
Плоскость Р в пространстве можно задать некоторой ее точкой М0(х 0, у 0, z 0) и ненулевым вектором n = (А,В,С), перпендикулярным плоскости. Этими условиями определяется единственная плоскость в пространстве. Вектор n = (А,В,С) называется нормальным вектором плоскости.
Возьмем произвольную точку М(х,у,z). Точка М принадлежит плоскости тогда и только тогда, когда векторы 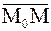 и n ортогональны. Используя условие ортогональности векторов n = (А,В,С) и
и n ортогональны. Используя условие ортогональности векторов n = (А,В,С) и
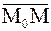 = (
= (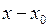 ,
,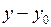 ,
,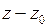 ), получаем, что точка М(х,у,z) принадлежит плоскости Р тогда и только тогда, когда скалярное произведение этих векторов равно нулю, т.е.
), получаем, что точка М(х,у,z) принадлежит плоскости Р тогда и только тогда, когда скалярное произведение этих векторов равно нулю, т.е.
А(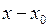 ) + В(
) + В(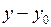 ) + С(
) + С(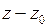 ) = 0. (2.22)
) = 0. (2.22)
Это и есть уравнение плоскости Р, так как ему удовлетворяют координаты х,у,z любой точки М, принадлежащей плоскости Р, и не удовлетворяют координаты точки, не принадлежащей этой плоскости.
|
|
|
Уравнение плоскости, записанное в виде
А х +В у +С z +D =0 (2.23)
(где D = –А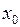 –В
–В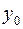 –С
–С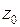 и
и 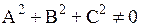 ), называется общим уравнением плоскости и представляет собой уравнение первой степени относительно текущих координат х,у,z. Таким образом, плоскость есть поверхность первого порядка.
), называется общим уравнением плоскости и представляет собой уравнение первой степени относительно текущих координат х,у,z. Таким образом, плоскость есть поверхность первого порядка.
Пусть теперь дано уравнение (2.23), причем хотя бы один из коэффициентов А, В или С не равен нулю (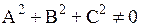 ). Выберем некоторую точку М0(х 0, у 0, z 0), лежащую на поверхности (2.23) (например, если А ≠ 0, то в качестве такой точки можно взять
). Выберем некоторую точку М0(х 0, у 0, z 0), лежащую на поверхности (2.23) (например, если А ≠ 0, то в качестве такой точки можно взять
М0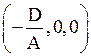 . Имеем
. Имеем
А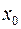 +В
+В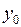 +С
+С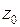 +D = 0. (2.24)
+D = 0. (2.24)
Вычитая из уравнения (2.23) уравнение (2.24), получим уравнение
А(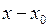 )+В(
)+В(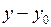 )+С(
)+С(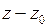 ) = 0, (2.25)
) = 0, (2.25)
эквивалентное данному. Полученное уравнение (а значит, и уравнение (2.23)) совпадает с уравнением (2.22). Следовательно, поверхность, заданная уравнением (2.22), является плоскостью, проходящей через точку М0(х 0, у 0, z 0) перпендикулярно вектору n.
Если D = 0, то уравнение А х + В у + С z = 0 определяет плоскость, проходящую через начало координат. Другие частные случаи определяются расположением нормального вектора
n = (А,В,С) Так, например, если А = 0, то уравнение В у +С z +D = 0 определяет плоскость, параллельную оси Ох; если А = D = 0, то уравнение В у +С z = 0 определяет плоскость, проходящую через ось Ох; если А = В = 0, то уравнение С z + D = 0 определяет плоскость, параллельную плоскости Оху; если А = В = D = 0, то 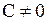 и уравнение С z = 0 (или z = 0) определяет координатную плоскость Оху.
и уравнение С z = 0 (или z = 0) определяет координатную плоскость Оху.
Условия параллельности и перпендикулярности плоскостей определяются условиями коллинеарности и перпендикулярности нормальных векторов n 1 = (А1,В1,С1) и n 2 = (А2,В2,С2).
Условием параллельности двух плоскостей Р и Р¢ является пропорциональность коэффициентов при одноименных переменных
|
|
|
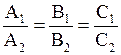 , (2.26)
, (2.26)
Условием перпендикулярности плоскостей Р и Р¢ является равенство нулю скалярного произведения нормальных векторов этих плоскостей
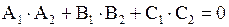 .
.
Заметим, что если для плоскостей не выполнено условие (2.26), то эти плоскости не параллельны и не сливаются, т.е. являются пересекающимися.
Прямая в пространстве может быть задана как линия пересечения двух плоскостей, т.е. как множество точек, координаты которых удовлетворяют системе
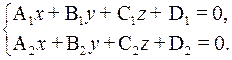
Если прямая параллельна ненулевому вектору a = (m,n,p) (называемому направляющим вектором прямой) и проходит через точку М1(х 1, у 1, z 1), то ее уравнения могут быть получены из условия
коллинеарности векторов 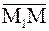 = (
= (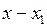 ,
,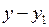 ,
,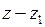 ) (где М(х,у,z) – произвольная точка прямой) и a = (m,n,p):
) (где М(х,у,z) – произвольная точка прямой) и a = (m,n,p): 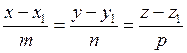 .
.
 2014-02-12
2014-02-12 1972
1972
