Система n линейных уравнений с n неизвестными

Для системы (5.6) с квадратной матрицей А составим следующие определители:

D=detА=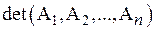– определитель матрицы системы (5.6);

D₁=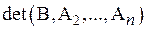– определитель матрицы, полученной из матрицы системы заменой ее первого столбца столбцом свободных членов;

D₂=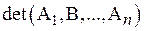– определитель матрицы, полученной из матрицы системы заменой ее второго столбца столбцом свободных членов;

……………

D_n=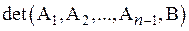– определитель матрицы, полученной из матрицы системы заменой ее n -го столбца столбцом свободных членов.

Теорема 5.3. Если определитель D матрицы системы n линейных уравнений с n неизвестными не равен нулю, то система имеет единственное решение К = (),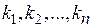

где 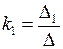, , 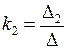…, 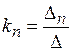. (5.8)

□ Система n линейных уравнений с n неизвестными в векторной форме имеет вид (5.4): 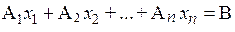. Так как определитель системы не равен нулю, то из теоремы 5.2 следует, что данная система уравнений имеет единствнное решение, которое обозначим через К = (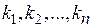). Подставив это решение в уравнение (5.4), получим верное векторное равенство: .

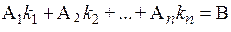Докажем сначала, что 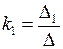. Заменим в определителе D₁ столбец В равным ему столбцом :

.

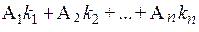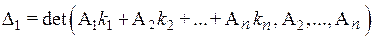Используя свойства определителей, имеем

==

=.

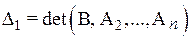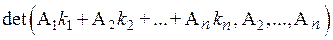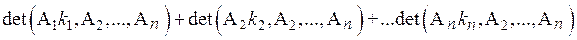В последнем равенстве все определители, кроме первого, содержат пропорциональные столбцы, и, следовательно, равны нулю. В первом определителе вынесем множитель 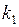. Получим

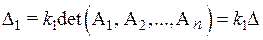, откуда .

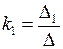Справедливость остальных формул (5.8) можно установить аналогично.

Таким образом, мы доказали, что если существует решение 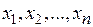системы n линейных уравнений с n неизвестными с определителем 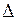матрицы системы, отличным от нуля, то это решение однозначно определяется формулами (5.8). ■

Формулы (5.8) называются формулами Крамера, а система (5.6) с ненулевым определителем 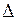– разрешимой по формулам Крамера.

Пример. Решить систему уравнений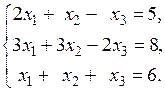

○ Вычислим определитель D матрицы системы и определители D₁,D₂,D₃.

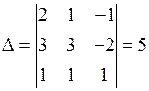, D ¹ 0, ,

, .

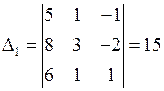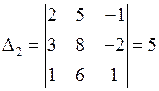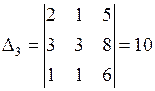По формулам Крамера находим:

, , . ●

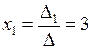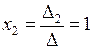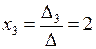Решение систем n линейных уравнений с n неизвестными по формулам Крамера требует вычисления (n +1) определителя n -го порядка, что уже достаточно трудоемко даже при n = 4. Поэтому этот метод представляет скорее теоретический интерес.