Лекция 11
Рассмотрим неоднородное линейное дифференциальное уравнение вида
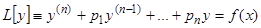 , (1)
, (1)
где 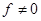 .
.
Однородное линейное уравнение с теми же коэффициентами, но с правой частью, равной нулю,
 , (2)
, (2)
называется однородным уравнением, соответствующим неоднородному уравнению (1). Очевидно, уравнения (1) и (2) не имеют общих решений.
Неоднородное уравнение, сохраняя прежние обозначения, кратко запишем в виде 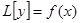 . Если при
. Если при 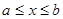 в уравнении (1) все коэффициенты
в уравнении (1) все коэффициенты 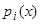 и правая часть
и правая часть 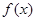 непрерывны, то оно имеет единственное решение, удовлетворяющее условиям
непрерывны, то оно имеет единственное решение, удовлетворяющее условиям 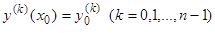 , где
, где  — любые действительные числа, а
— любые действительные числа, а 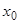 — любая точка интервала
— любая точка интервала 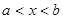 .
.
Действительно, правая часть уравнения 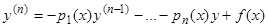 в окрестности рассматриваемых начальных значений удовлетворяет условиям теоремы существования и единственности:
в окрестности рассматриваемых начальных значений удовлетворяет условиям теоремы существования и единственности:
1) правая часть непрерывна по всем аргументам;
2) имеет ограниченные частные производные по всем 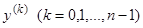 , так как эти производные равны непрерывным по предположению на отрезке
, так как эти производные равны непрерывным по предположению на отрезке 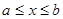 коэффициентам
коэффициентам 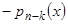 . Еще раз отметим, что на начальные значения
. Еще раз отметим, что на начальные значения  не налагается никаких ограничений.
не налагается никаких ограничений.
Из двух основных свойств линейного оператора непосредственно следует:
1) Сумма решения 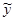 неоднородного уравнения (1) и решения
неоднородного уравнения (1) и решения 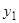 соответствующего однородного уравнения
соответствующего однородного уравнения 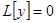 является решением неоднородного уравнения (1).
является решением неоднородного уравнения (1).
Доказательство.  , но
, но 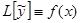 , а
, а 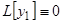 , следовательно
, следовательно  .
.
2) Если  является решением уравнения
является решением уравнения 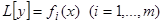 , то
, то 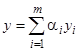 является решением уравнения
является решением уравнения 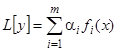 , где
, где 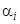 — постоянные.
— постоянные.
Доказательство.
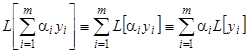 , (2.1)
, (2.1)
но 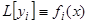 , следовательно,
, следовательно, 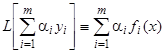 .
.
Это свойство, называемое часто принципом суперпозиции (или принципом наложения), очевидно, остается справедливым и при 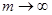 , если ряд
, если ряд 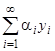 сходится и допускает
сходится и допускает  -кратное почленное дифференцирование, так как в этом случае возможен предельный переход в тождествах (2.1).
-кратное почленное дифференцирование, так как в этом случае возможен предельный переход в тождествах (2.1).
3) Если уравнение 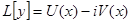 , где все коэффициенты
, где все коэффициенты 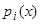 и функции
и функции 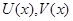 действительны, имеет решение
действительны, имеет решение 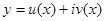 , то действительная часть решения
, то действительная часть решения 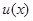 и мнимая часть
и мнимая часть 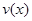 являются соответственно решениями уравнений
являются соответственно решениями уравнений 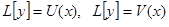 .
.
Доказательство.  или
или 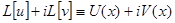 . Следовательно, отдельно равны действительные части
. Следовательно, отдельно равны действительные части  и мнимые части
и мнимые части 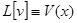 .
.
Теорема. Если известно какое-нибудь частное решение  неоднородного уравнения (1), то общее его решение есть сумма этого частного решения и общего решения соответствующего однородного уравнения.
неоднородного уравнения (1), то общее его решение есть сумма этого частного решения и общего решения соответствующего однородного уравнения.
Так как  есть решение уравнения (1), то имеем тождество
есть решение уравнения (1), то имеем тождество
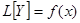 ; (3)
; (3)
введем новую искомую функцию 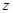 , полагая
, полагая
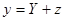 . (4)
. (4)
Подставляя выражение (4) в уравнение (1), имеем, в силу первого свойства линейного оператора 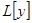 ,
, 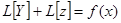 . Принимая во внимание тождество (3), получаем отсюда
. Принимая во внимание тождество (3), получаем отсюда 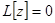 — однородное уравнение, соответствующее (1).
— однородное уравнение, соответствующее (1).
Пусть фундаментальная система уравнения (2), соответствующего уравнению (1), будет 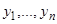 . Тогда общее решение уравнения (2) имеет вид
. Тогда общее решение уравнения (2) имеет вид 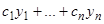 . Подставляя это выражение вместо
. Подставляя это выражение вместо 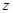 в формулу (4), получаем общее решение неоднородного уравнения (1)
в формулу (4), получаем общее решение неоднородного уравнения (1)
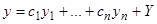 . (5)
. (5)
Это уравнение содержит  произвольных постоянных. Чтобы доказать, что эти постоянные существенные, покажем, что из выражения (26) принадлежащем выборе значений постоянных
произвольных постоянных. Чтобы доказать, что эти постоянные существенные, покажем, что из выражения (26) принадлежащем выборе значений постоянных  получится решение, удовлетворяющее любым начальным условиям Коши, т.е. при
получится решение, удовлетворяющее любым начальным условиям Коши, т.е. при 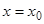 , где
, где 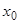 — любое значение из интервала
— любое значение из интервала 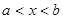 , мы будем иметь
, мы будем иметь 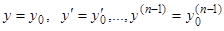 , где
, где 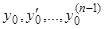 — любая данная система
— любая данная система  чисел. Последовательным дифференцированием выражения (5) находим
чисел. Последовательным дифференцированием выражения (5) находим
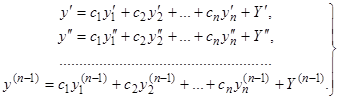 (5.1)
(5.1)
В выражениях (5) и (5.1) надо в левых частях вместо 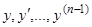 подставить соответственно
подставить соответственно 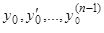 , а в правых частях во всех функциях дать переменной
, а в правых частях во всех функциях дать переменной  значение
значение 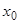 . Получится система
. Получится система  линейных уравнений с
линейных уравнений с  неизвестными
неизвестными  . Определитель этой системы есть значение определителя Вронского
. Определитель этой системы есть значение определителя Вронского 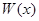 при
при 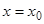 . При этом
. При этом 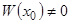 , так как система
, так как система 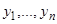 , по предположению, фундаментальная. Таким образом, для
, по предположению, фундаментальная. Таким образом, для  получим вполне определенные значения, и решение (5), действительно, является общим. Теорема доказана.
получим вполне определенные значения, и решение (5), действительно, является общим. Теорема доказана.
Пример 1. Рассмотрим уравнение 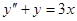 . Легко видеть, что частным решением будет
. Легко видеть, что частным решением будет 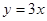 . Соответствующее однородное уравнение
. Соответствующее однородное уравнение 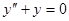 имеет два линейно независимых частных решения:
имеет два линейно независимых частных решения: 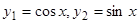 . В силу рассмотренного общее решение будет
. В силу рассмотренного общее решение будет  . Решим теперь для данного уравнения задачу Коши: найти решение, удовлетворяющее начальным условиям
. Решим теперь для данного уравнения задачу Коши: найти решение, удовлетворяющее начальным условиям  при
при  . Имеем:
. Имеем: 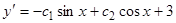 . Подставляя начальные значения, находим
. Подставляя начальные значения, находим  , откуда
, откуда 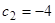 . Искомое решение есть
. Искомое решение есть 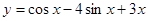 .
.
Пусть, далее, известно одно частное решение 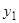 однородного уравнения (2), соответствующего уравнению (1). Подобно тому, как в случае однородного уравнения, применяем подстановку
однородного уравнения (2), соответствующего уравнению (1). Подобно тому, как в случае однородного уравнения, применяем подстановку 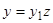 и получаем уравнение, не содержащее явно искомой функции
и получаем уравнение, не содержащее явно искомой функции 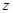 . После этого, полагая
. После этого, полагая 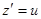 , получим неоднородное линейное уравнение порядка
, получим неоднородное линейное уравнение порядка 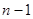 . Итак, если известно одно частное решение соответствующего однородного уравнения, преобразование переменной
. Итак, если известно одно частное решение соответствующего однородного уравнения, преобразование переменной 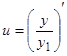 понижает порядок неоднородного уравнения на единицу. Также аналогично случаю однородного уравнения получается следующий результат: если известны
понижает порядок неоднородного уравнения на единицу. Также аналогично случаю однородного уравнения получается следующий результат: если известны 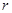 частных линейно независимых решений соответствующего однородного уравнения, то порядок неоднородного уравнения может быть понижен на
частных линейно независимых решений соответствующего однородного уравнения, то порядок неоднородного уравнения может быть понижен на 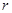 единиц.
единиц.
Предположим теперь, что известны 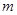 частных решений неоднородного уравнения (1)
частных решений неоднородного уравнения (1) 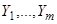 . Введем новую искомую функцию
. Введем новую искомую функцию 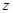 , связанную с
, связанную с  уравнением
уравнением 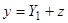 или
или  .
.
Как было показано, 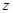 удовлетворяет однородному уравнению, которое соответствует неоднородному уравнению (1). Подставляя вместо
удовлетворяет однородному уравнению, которое соответствует неоднородному уравнению (1). Подставляя вместо  функции
функции 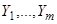 , мы, кроме тривиального решения
, мы, кроме тривиального решения 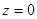 , получим
, получим 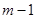 решений однородного уравнения:
решений однородного уравнения: 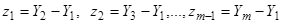 . Таким образом, нам известны
. Таким образом, нам известны 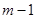 решений однородного уравнения (2), и если они линейно независимы, то его порядок может быть понижен на
решений однородного уравнения (2), и если они линейно независимы, то его порядок может быть понижен на 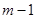 единиц. Итак, если известны
единиц. Итак, если известны 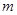 частных решений неоднородного линейного уравнения, то при указанном условии его интегрирование приводится к интегрированию линейного однородного уравнения порядка
частных решений неоднородного линейного уравнения, то при указанном условии его интегрирование приводится к интегрированию линейного однородного уравнения порядка 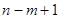 .
.
Пример 2. Уравнение 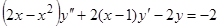 имеет, как легко проверить, два частных решения:
имеет, как легко проверить, два частных решения: 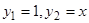 . Следовательно, соответствующее однородное уравнение имеет решение
. Следовательно, соответствующее однородное уравнение имеет решение 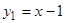 . Комбинируя подстановки (4) и
. Комбинируя подстановки (4) и 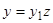 , вводим новую искомую функцию
, вводим новую искомую функцию 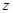 при помощи уравнения
при помощи уравнения 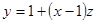 , откуда
, откуда 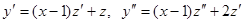 . Подставляя полученные выражения в данное уравнение, находим:
. Подставляя полученные выражения в данное уравнение, находим: 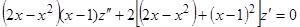 , откуда
, откуда  . Подставляя в выражение для
. Подставляя в выражение для  , получаем
, получаем 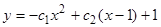 — общее решение.
— общее решение.
Метод вариации произвольных постоянных. Как мы уже знаем, для решения неоднородного уравнения достаточно знать фундаментальную систему решений соответствующего однородного уравнения и одно частное решение неоднородного уравнения.
Теперь мы докажем следующую теорему: если известна фундаментальная система соответствующего однородного уравнения, то общее решение неоднородного уравнения может быть найдено при помощи квадратур.
Мы дадим способ решения неоднородного уравнения, называемый методом вариации произвольных постоянных.
Пусть дано неоднородное линейное уравнение
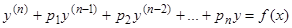 , (1)
, (1)
где 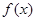 не равно тождественно нулю, и пусть нам известна фундаментальная система
не равно тождественно нулю, и пусть нам известна фундаментальная система 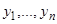 соответствующего однородного уравнения
соответствующего однородного уравнения
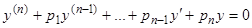 . (2)
. (2)
Общее решение уравнения (2), как мы знаем, будет
 , (2.1)
, (2.1)
где  — произвольные постоянные. Выражение (2.1) удовлетворяет уравнению (2) и, следовательно, не может удовлетворять уравнению (1), пока
— произвольные постоянные. Выражение (2.1) удовлетворяет уравнению (2) и, следовательно, не может удовлетворять уравнению (1), пока 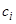 остаются постоянными. Поставим себе цель — получить решение уравнения (1) в той же форме (2.1), где, однако,
остаются постоянными. Поставим себе цель — получить решение уравнения (1) в той же форме (2.1), где, однако,  будут функциями независимой переменной
будут функциями независимой переменной  . Мы получаем
. Мы получаем  новых неизвестных функций. Для их определения нужно иметь
новых неизвестных функций. Для их определения нужно иметь  уравнений. Одно из них получится из условия, что выражение (2.1) (уже с переменными
уравнений. Одно из них получится из условия, что выражение (2.1) (уже с переменными 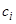 ) удовлетворяет уравнению (1), а остальные
) удовлетворяет уравнению (1), а остальные 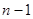 уравнений мы можем задать произвольно. Мы их будем задавать таким образом, чтобы выражения для производных от
уравнений мы можем задать произвольно. Мы их будем задавать таким образом, чтобы выражения для производных от  имели наиболее простой вид.
имели наиболее простой вид.
Дифференцируем равенство (2.1) по  :
: 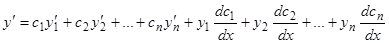 . Мы записали слагаемые, полученные от дифференцирования, в две группы: в качестве первого из
. Мы записали слагаемые, полученные от дифференцирования, в две группы: в качестве первого из 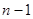 дополнительных уравнений возьмем уравнение, которое получится, если вторую группу приравнять нулю:
дополнительных уравнений возьмем уравнение, которое получится, если вторую группу приравнять нулю:
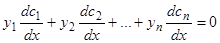 . (6.1)
. (6.1)
В таком случае для  получим выражение
получим выражение
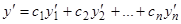 , (7.1)
, (7.1)
которое имеет такой же вид, как и в случае постоянных 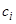 .
.
Для нахождения 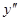 опять дифференцируем равенство (7.1) по
опять дифференцируем равенство (7.1) по  . В полученном результате опять приравниваем нулю слагаемые, содержащие производные функций
. В полученном результате опять приравниваем нулю слагаемые, содержащие производные функций 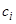 (это будет второе добавочное уравнение):
(это будет второе добавочное уравнение):
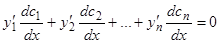 , (6.2)
, (6.2)
и для 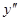 получится выражение
получится выражение
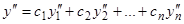 . (7.2)
. (7.2)
Продолжая таким образом, мы в последний раз введем добавочное условие на 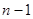 -м шаге:
-м шаге:
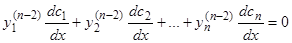 , (6.n-1)
, (6.n-1)
и выражение для  будет иметь вид
будет иметь вид
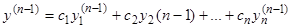 . (7.n-1)
. (7.n-1)
Вычисляем, наконец, 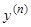 :
:
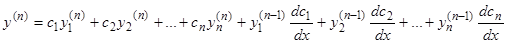 . (7.n)
. (7.n)
Подставляя выражения (2.1), (7.1), …, (7.n-1), (7.n) в уравнение (1), получаем
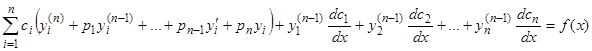 .
.
Замечаем, что множители при 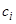 под знаком суммы все равны нулю, так как они являются результатами подстановки в левую часть уравнения (2) его решений, и мы получаем последнее уравнение для определения
под знаком суммы все равны нулю, так как они являются результатами подстановки в левую часть уравнения (2) его решений, и мы получаем последнее уравнение для определения 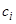 :
:
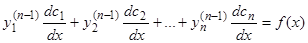 . (6.n)
. (6.n)
Мы получили систему  неоднородных линейных уравнений (6.1), (6.2), … (6.n-1), (6.n) с
неоднородных линейных уравнений (6.1), (6.2), … (6.n-1), (6.n) с  неизвестными
неизвестными 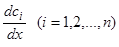 . Определитель этой линейной системы есть определитель Вронского для фундаментальной системы; он не обращается в нуль. Следовательно, разрешая ее, мы получим
. Определитель этой линейной системы есть определитель Вронского для фундаментальной системы; он не обращается в нуль. Следовательно, разрешая ее, мы получим 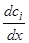 как известные непрерывные функции от
как известные непрерывные функции от  :
: 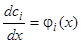 , откуда квадратурами находим
, откуда квадратурами находим 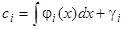 (
(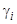 — новые произвольные постоянные).
— новые произвольные постоянные).
Подставляя найденные значения 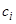 в выражение (2.1), мы найдем общее решение уравнения (1):
в выражение (2.1), мы найдем общее решение уравнения (1): 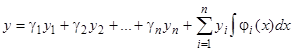 . Действительно, по самому его образованию это есть решение рассматриваемого уравнения. Сумма слагаемых, содержащих множители
. Действительно, по самому его образованию это есть решение рассматриваемого уравнения. Сумма слагаемых, содержащих множители 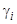 , представляет собой, как мы знаем, общее решение однородного уравнения (2), а выражение
, представляет собой, как мы знаем, общее решение однородного уравнения (2), а выражение 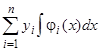 есть частное решение неоднородного уравнения (1). Таким образом, действительно, при знании фундаментальной системы однородного уравнения мы получаем с помощью квадратур решение неоднородного уравнения.
есть частное решение неоднородного уравнения (1). Таким образом, действительно, при знании фундаментальной системы однородного уравнения мы получаем с помощью квадратур решение неоднородного уравнения.
Пример 3. Рассмотрим уравнение 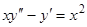 . Соответствующее однородное уравнение
. Соответствующее однородное уравнение 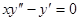 легко интегрируется:
легко интегрируется: 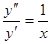 ,
, 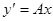 ,
, 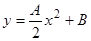 . Его фундаментальная система есть
. Его фундаментальная система есть 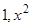 . Полагаем теперь в неоднородном уравнении
. Полагаем теперь в неоднородном уравнении 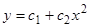 . Для определения
. Для определения 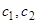 имеем два уравнения:
имеем два уравнения: 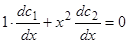 ,
, 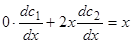 . (Обратим внимание, что формула (6.n) выведена в предположении, что коэффициент при старшей производной равен 1). Последовательно получаем
. (Обратим внимание, что формула (6.n) выведена в предположении, что коэффициент при старшей производной равен 1). Последовательно получаем 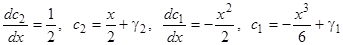 . Подставляя в выражение для
. Подставляя в выражение для  , находим общее решение:
, находим общее решение: 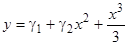 (
(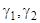 — произвольные постоянные).
— произвольные постоянные).
Рассмотрим еще метод Коши нахождения частного решения линейного неоднородного уравнения
 . (8)
. (8)
В этом методе предполагается известным, зависящее от одного параметра, решение 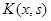 соответствующего однородного уравнения
соответствующего однородного уравнения 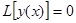 , удовлетворяющее условиям
, удовлетворяющее условиям
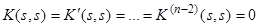 , (9)
, (9)
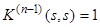 . (10)
. (10)
Нетрудно проверить, что в этом случае
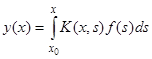 (11)
(11)
будет частным решением уравнения (8), удовлетворяющим нулевым начальным условиям  . Действительно, дифференцируя (11) и принимая во внимание условия (9) и (10), получим
. Действительно, дифференцируя (11) и принимая во внимание условия (9) и (10), получим
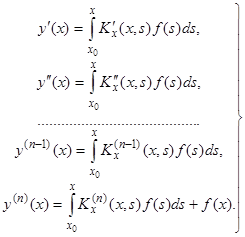 (12)
(12)
Подставляя (11) и (12) в уравнение (8), получаем 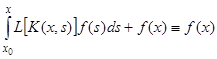 , так как
, так как 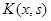 является решением соответствующего однородного уравнения и
является решением соответствующего однородного уравнения и 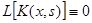 .
.
Решение 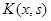 может быть выделено из общего решения
может быть выделено из общего решения 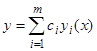 однородного уравнения, если выбрать произвольные постоянные
однородного уравнения, если выбрать произвольные постоянные 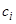 так, чтобы удовлетворялись условия (9) и (10).
так, чтобы удовлетворялись условия (9) и (10).
Пример 4. Для уравнения 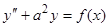 общим решением является
общим решением является 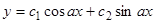 . Условия (9) и (10) приводят к следующим уравнениям:
. Условия (9) и (10) приводят к следующим уравнениям:  . Следовательно,
. Следовательно, 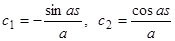 , и искомое решение
, и искомое решение 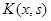 имеет вид
имеет вид 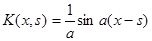 . Решение исходного уравнения, удовлетворяющее нулевым начальным условиям, согласно (11), представимо в виде
. Решение исходного уравнения, удовлетворяющее нулевым начальным условиям, согласно (11), представимо в виде 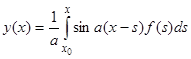 .
.
 2014-02-02
2014-02-02 1804
1804
