Чтобы произвести расчет САУ, надо иметь математическую модель системы. Обычно математической моделью является дифференциальное уравнение, которое получают, анализируя физический, механический или иной процесс.
Рассмотрим математическую модель разомкнутой системы, которая выражается дифференциальным уравнением общего вида:
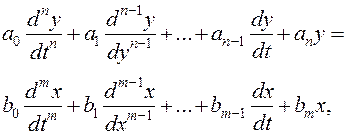 (2.1)
(2.1)
где y –управляемая величина, x – управляющая величина; обе – функции времени;коэффициенты ai, bi – постоянные. Правая часть описывает воздействие, левая часть – изменение управляемой величины.
Решение уравнения (2.1) дает полное представление об изменении управляемой величины.
Однако в теории автоматического управления предпочитают иметь дело не с дифференциальным уравнением, а с операторным уравнением, точнее – с его особой формой, которая получила название «передаточная функция».
Операторное уравнение получают, применяя преобразование Лапласа к дифференциальному уравнению.
Суть преобразования Лапласа в том, что функцию от времени преобразуют в функцию от комплексного временного 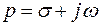 (
(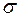 - действительная часть, w - мнимая часть, j =
- действительная часть, w - мнимая часть, j = 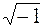 ). Функцию от времени называют «оригинал», а ее преобразование по Лапласу – «изображение». Для изображения используют прописные буквы.
). Функцию от времени называют «оригинал», а ее преобразование по Лапласу – «изображение». Для изображения используют прописные буквы.
Символически преобразование Лапласа принято обозначать прописной буквой L. Например,
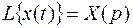 ,
,  ,
, 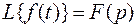 .
.
(Читается: «изображение функции x (t) есть X (p)» и т. д.)
При преобразовании Лапласа коэффициенты-множители не меняются, а изображение производной представляется произведением комплексного переменного p на изображение функции. Например,
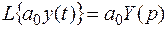 ,
, 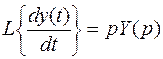 .
.
Более высокие производные представляются произведением p в соответствующей степени на изображение функции:
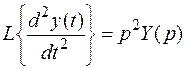 ,
, 
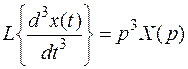 и т. п.
и т. п.
Формально оператор дифференцирования заменяется комплексной переменной p в соответствующей степени:
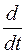 на p,
на p, 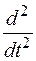 на p 2,
на p 2, 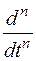 на pn.
на pn.
Преобразование Лапласа, будучи применено к дифференциальному уравнению, преобразует его в алгебраическое. Например,
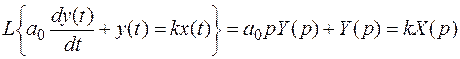 .
.
Обратный переход из комплексного пространства во временное достигается обратными преобразованием Лапласа, символ L -1. Например,
 ,
, 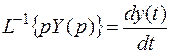 и т. д.
и т. д.
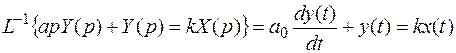 .
.
Дополнительно о преобразовании Лапласа рекомендуется прочитать в Приложении 1. В Приложении 2 дана таблица, показывающая преобразование Лапласа некоторых функций.
Применив преобразование Лапласа к дифференциальному уравнению общего вида (2.1), получаем
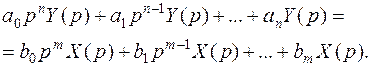
Или
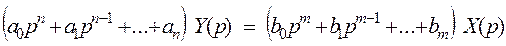 (2.2)
(2.2)
Введем обозначения:
b 0 pm + b 1 pm -1 +…+ bm -1 p + bm = В (p), (2.3)
a 0 pn + a 1 pn -1 +…+ an -1 p + an = D (p). (2.4)
Комплексный полином В(р) описывает управляющее воздействие на систему. Комплексный полином D(p) описывает изменение управляемой величины. Введенные обозначения позволяют представить уравнение (2.2) краткой записью:
D(p) Y(p) = B(p) X(p).
Уравнение (2.2) и его краткую запись называют операторным уравнением.
Особую роль в математическом описании линейных систем автоматического управления играет отношение Y(p) / X(p). Его называют передаточной функцией и обозначают W(p).
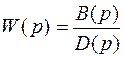 . (2.5)
. (2.5)
Уточним, что выражение (2.5) является передаточной функцией разомкнутой системы, поскольку получено из дифференциального уравнения (2.1), записанного для разомкнутой системы.
Операторное уравнение можно записывать, используя передаточную функцию:
Y (p) = W (p) X (p). (2.6)
Как было сказано, комплексный полином D (p) описывает изменение управляемой величины. То есть, характеризует процесс, который происходит в системе под влиянием управляющего воздействия. Поэтому полином D (p) называют характеристическим. Приравнивая его к нулю, получают характеристическое уравнение системы:
a 0 pn + a 1 pn -1 + …+ an -1 p + an = 0. (2.7)
Характеристическое уравнение позволяет найти корни и получить решение дифференциального уравнения. Характеристический полином, характеристическое уравнение служат основой исследования системы на устойчивость.
Для преобразования Лапласа необходимо, чтобы начальные условия были нулевыми, а дифференциальные уравнения – линейными. Однако, линейность уравнений, описывающих реальные технические системы, скорее исключение, чем правило. В случае слабо нелинейной зависимости (типа слабо искривленной линии, участок которой можно заменить прямой с пренебрежимой погрешностью), осуществляют линеаризацию и ведут расчеты на отрезке прямой.
 2014-02-02
2014-02-02 4071
4071