Лекция 3. Работа по перемещению заряда в электрическом поле. Потенциал электростатического поля

§ 3 – 1. Работа по перемещению заряда в электрическом поле.

Как уже отмечалось, на электрический заряд q со стороны поля, созданного зарядом Q,

действует кулоновская сила. Поэтому при перемещении заряда q в поле совершается рабо-та,величина которой определяется выражением dA = F_ldlcosa, где a - угол между направ-

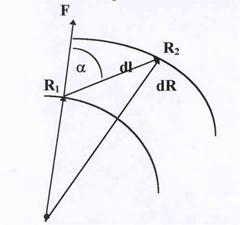Рис.8. К расчету элементарной работы.

лениями силы и перемещения (см. рис 8).Учитывая, что Fcosa = Fl имеем dA = Fldl. Для нашего случая F = qE; qE = 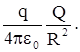Из рис. видно, что dlcosa =dR, и малая работа в поле равна d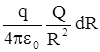A = ; A = 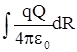= 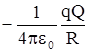. Из полученной форулы следует, что работа по пере-мещению заряда в поле не зависит от формы пути, т.е. электростатические силы являются потенциальными. Следовательно, заряд в поле обладает потенциальной энергией. Работа при изменении расстояния от R1 до R2 равна

= .

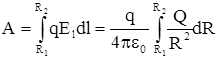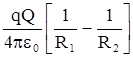Из независимости работы от формы пути перемещения следует, что работа электро-статических сил по замкнутому пути равна нулю. В этом случае в первом интеграле величину заряда q, вынесенную за знак интегрирования, можно сократить. Тогда

.

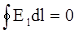В этой формуле интеграл с кружком обозначает так называемую циркуляцию, т.е. он обоз-начает, что интегрировапние проводится по замкнутому контуру. Справедливость этого утверждения следует из непосредственного выражения для элементарной работы при прод-

вижении вдоль элементарного перемещения dl: dA = Edlcosa =E_l dl, где a - угол между направлением силы и перемещения.

§ 3 – 2 Потенциал электрического поля.

Как уже отмечалось, пробный заряд в электрическом поле обладает потенциальной энергией. Однако величина этой энергии зависит от величины заряда q. Для того, чтобы можно было охарактеризовать само поле, условились относить величину потенциальной энергии заряда q к величине этого заряда. Эту величину принято называть потенциалом электрического поля. Здесь необходимо напомнить, что само определение потенциальной энергии содержит в себе неоднозначность, т.к. эта энергия определена с точностью до некоторой постоянной. Для однозначной характеристики электрического поля принято определять эту постоянную при удалении заряда q на бесконечность. Считается, что два за-ряда, удаленные друг от друга на бесконечность, не взаимодействуют, т.е. их энергия взаимодействия и, следовательно, постоянная равны нулю. Поэтому можно сказать, что по-тенциалом электрического поля j называется работа по перемещению единичного положительного заряда из данной точки поля в бесконечность. Из выражения для работы А следует, что потенциал j равен

j =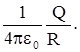

Потенциал – величина скалярная, он удовлетворяет принципу суперпозиции, т.е. потенциал от суммы зарядов равен сумме потенциалов от каждого заряда в отдельности. Если заряд q равный 1 Кулону, перемещается из одной точки поля в другую, то соответствующую работу называют разностью потенциалов или напряжением U, т.е.

Dj =U =;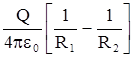

где R₁ и R₂ соответствуют начальному и конечному положению единичного положитель-ного зваряда. Единицей напряжения, как известно, служит один Вольт. При перемещении произвольного заряда q величина совершаемой работы увеличивается в q раз.

Связь между потенциалом и напряженностью электрического поля.

Связь между потенциалом и напряженностью поля легко установить из выражения для элементарной работы dA. Так dA можно записать через напряженность поля Е и перемещение dl: dA = qEcosbdl, где b - угол между Е и dl. С другой стороны, используя определение потенциала, работа dA = qdj. Из этих выражений следует, что dj = Ecosbdl =

= E_l dl, и

j = .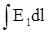

Обратная связь между напряженностью и приращением потенциала должна иметь вид 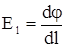, однако следует отметить, что напряженность поля – вектор. Поэтому производная 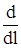должна иметь смысл производной по направлению. Для положительного заряда вектора напряженности положительны и направлены от заряда и в сторону умень-шения потенциала. Поэтому перед производной необходимо поставить знак минус, т.е.

.

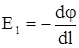Из этого выражения видно, что величина производной зависит от угла между Е и dl. Так для направления, перпендикулярного Е, проекция E_l равна нулю; наоборот, для направле-ния вдоль Е производная по dl максимальна и равна Е, т.е.

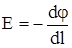_{в направлении Е}.

Термин «производная по направлению» становится более понятным в применении к прямо-угольным координатам. Рассматривая поочередно проекции Е на оси x,y и z можно напи-сать:

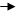
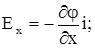
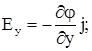
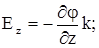
где i, j, и k - единичные вектора вдоль осей x, y и z соответственно. Сам вектор Е нахо-дится как сумма:

E = Е_х + Е_у + Е_z.

В теории поля производная по направлению наибольшего изменения функции называется градиентом (grad), т.е. связь между напряженностью и потенциалом имеет вид:

E = - grad j.

В направлении, перпендикулярном вектору Е, величина производной от потенциала рав-на нулю, т.е. в этом направлении потенциал остается постоянным. Линии или поверхности, соединяющие точки с одинаковыми потенциалами, принято называть эквипотенциальны-ми. Примером топологии эквипотенциалей может служить рис.2 предыдущей лекции. Соотношение Е = - Dj ¤D l показывает, что напряженность поля можно измерять в единицах Вольт / метр.