Электростатическое поле, напряженность, индукция, потенциал.
План лекции:
4. Электромагнитное поле как вид материи, понятие,,поле”.
5. Электростатическое поле как частный случай электромагнитного поля, электрический заряд как источник поля.
6. Электростатическое поле в вакууме. Закон Кулона, напряженность электростатического поля, индукция поля.
7. Потенциал электростатического поля, понятие потенциального поля; связь между напряженностью и потенциалом потенциального поля.
Краткое содержание лекции
Электромагнитное поле является одним из видов материи, оно реально как троллейбус, имеет энергию, массу, перемещается в пространстве, используется в практической деятельности человека. Если электромагнитное поле создаётся неподвижным зарядом, то оно называется электростатическим. Этим полем начинается изучение электромагнитного поля, так проще усваивается материал и понимается.
Закон Шарля Кулона
Заряд обозначается q или 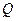 , измеряется в кулонах [Кл], бывает положительным или отрицательным.
, измеряется в кулонах [Кл], бывает положительным или отрицательным.
Кулон сообщил следующее:
1) заряды одноимённые отталкиваются, разноимённые – притягиваются;
2) сила взаимодействия двух зарядов пропорциональна их произведению 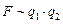 ;
;
3) сила взаимодействия двух зарядов пропорциональна квадрату расстояния между ними 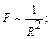
4) сила взаимодействия двух зарядов направлена по прямой, соединяющей точечные заряды или центры сферических зарядов;
5) сила взаимодействия двух зарядов зависит от свойств среды, в которой находятся эти заряды.
Итак, закон Кулона в аналитической форме имеет вид:
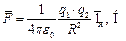
здесь 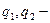 два взаимодействующих заряда;
два взаимодействующих заряда;
R – расстояние между зарядами;
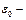 диэлектрическая постоянная
диэлектрическая постоянная 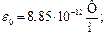
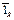 – единичный вектор, направленный вдоль линии, соединяющей заряды.
– единичный вектор, направленный вдоль линии, соединяющей заряды.
Электрическая сила относится к сильным силам, при 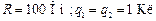 заряды взаимодействуют на расстоянии 1 км с силой 1000 кг.
заряды взаимодействуют на расстоянии 1 км с силой 1000 кг.
Величину поля можно оценивать по силе взаимодействия двух зарядов, один из которых является создающим поле (q), второй – пробным (q пр). Однако это не удобно, так как сила взаимодействия зависит от величины пробного заряда, поэтому в начале 20 века предложена другая оценка для интенсивности поля – напряженность поля:
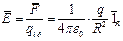 , В/м , В/м | (1) |
Напряженность является силовой характеристикой поля. Можно оценить поле с помощью такой величины как индукция, которая связана с напряженностью поля только множителем 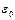 :
:
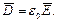
Однако индукция имеет иной физический смысл, нежели напряженность. Если в поле создаваемом зарядом q поместить металлическое тело, то на нём будут наводиться (индуцироваться) электрические заряды. Величина индуцированного заряда одного знака будет пропорциональна индукции
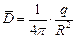 , Кл/м2
, Кл/м2
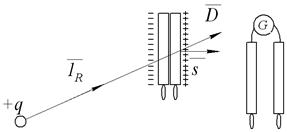
Рис. 1. Измерение индукции электростатического поля
В поле точечного заряда (рис. 1) расположены две пластины, находящиеся в контакте. Пластины имеют ручки из диэлектрика. Под действием поля источника положительные заряды уйдут в правую пластину. Левая пластина зарядится отрицательно. Затем пластины разъединяются, при этом через гальванометр протечет ток, пропорциональный величине заряда, накопленного на пластине. Будем проводить опыты, фиксируя величину тока. Пластины удаляются от источника, ток уменьшается обратно пропорционально квадрату расстояния R2. Кроме того, величина тока будет зависеть от ориентации площадок в пространстве, то есть от угла α. Установлено, что величина тока пропорциональна величине cos α. Естественно, что величина тока пропорциональна величине заряда q, образующего поле в пространстве. Пусть величина наводимого заряда (индуцированного) пропорциональна току i, т.е. q = k· i.
Так как 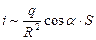 , или
, или 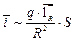 , то:
, то:
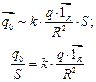
или
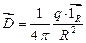
Здесь q0 – заряд, который протекает через гальванометр.
Поскольку 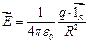 , то
, то 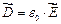 (для вакуума).
(для вакуума).
Для оценки интенсивности поля можно ввести ещё одну величину – потенциал. Если в поле, созданное зарядом q, вносить из бесконечности пробный заряд того же знака, что и q, то преодолевается некоторая сила отталкивания. Поэтому при перемещении пробного заряда из бесконечности (то есть оттуда, где нет поля) в точку с выполняется работа. По величине этой работы можно оценивать интенсивность поля. Величина работы равна:
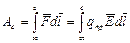 , Дж
, Дж
Однако величиной работы оценивать величину поля не совсем удобно, из-за необходимости учёта величины q пр. Поэтому используется для оценки поля не работа, а отношение работы к величине пробного заряда q пр, и это отношение называется потенциалом.
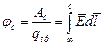 , В
, В
В общем случае величина потенциала связана с напряженностью поля зависимостью:
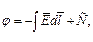 | (2) |
где С – произвольная постоянная.
Знак минус обусловлен тем, что величина потенциала в противоположном направлении с направлением вектора напряжённости поля 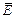 .
.
Кроме потенциала используется понятие разность потенциалов.
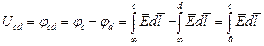 , В
, В
Разность потенциалов называется напряжением.
Учитывая (1) и (2) можно записать потенциал для точечного заряда
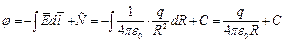 | (3) |
Если при R = ∞ φ = 0, то С = 0 и (3) запишется так: 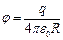
Если взять интеграл (2) по замкнутому контуру, то
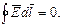 | (4) |
Поля, для которых выполняется условие (4), называются потенциальными. Для потенциальных полей величина интеграла (2) не зависит от пути интегрирования.
Если заряд не задан в точке, а распределён в пространстве, то вводится понятие объёмной плотности заряда в диэлектрике:
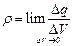 ,
, 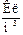 ,
,
где Δq – заряд в малом объёме ΔV.
Если заряд распределён по поверхности металлического тела, то вводится понятие поверхностной плотности заряда:
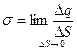 ,
, 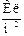 ,
,
где Δq – заряд на малой площадке поверхности металлического тела ΔS.
Если заряд распределён по длине линейного проводника, то существует понятие линейной плотности заряда:
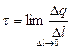 ,
, 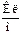 ,
,
где Δq – заряд на малом отрезке проводника 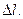
С учётом вышесказанного величину потенциала можно рассчитать по формулам:
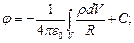 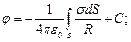 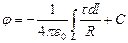 | (5) |
Здесь 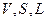 – полные объём заряда, поверхность металлического тела и длина металлического проводника.
– полные объём заряда, поверхность металлического тела и длина металлического проводника.
Формулы (5) являются решением уравнения Пуассона.
Для плоскопараллельного поля потенциал точечного заряда равен:
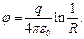
Контрольные вопросы:
1. Какие величины характеризуют интенсивность электростатического поля и каков их физический смысл?
2. Как рассчитать силу взаимодействия двух зарядов?
3. Как рассчитать потенциал точечного заряда электростатического поля?
4. Напишите формулы для расчёта потенциала поля, заданного объёмным зарядом, заряженным металлическим телом, отрезком проводника.
5. Что такое разность потенциалов?
 2014-02-02
2014-02-02 2997
2997
