Линейные преобразования

Определение: Будем считать, что в линейном пространстве L задано некоторое линейное преобразование А, если любому элементу 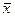Î L по некоторому правилу ставится в соответствие элемент А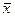Î L.

Определение: Преобразование А называется линейным, если для любых векторов 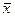Î L и 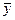Î L и любого a верно:

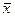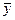A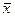(+) = A+A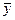

A(a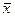) = aA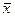

Пример. Является ли А линейным преобразованием. А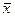=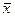+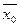; 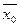¹ 0.

Запишем преобразование А для какого- либо элемент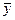а . А= +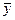

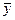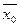
Проверим, выполняется ли правило операции сложения для этого преобразования А(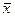+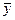) = 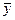++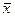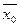; A(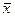) + A(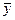) = 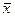++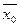+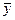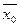, что верно только при 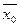= 0, т.е. данное преобразование А нелинейное.