Решение всех задач методом замены плоскостей проекций сводится к решению 4-х основных задач:
Первая задача: Заменить плоскость проекций так, чтобы прямая общего положения стала прямой уровня.
Вторая задача: Заменить плоскость проекций так, чтобы прямая уровня стала проецирующей прямой.
Решим обе задачи совместно:
Решение первой задачи: Пусть задана прямая общего положения отрезком [АВ]. Заменим плоскость V на V1
(V1 H)
H)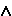 (V1
(V1 [AB])
[AB]) 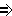 x1
x1 [A1B1]
[A1B1]
[A1A4] x1 [B1B4]
x1 [B1B4] x1
x1
B2Bx=Bx1B4 A2Ax=Ax1A4
|А4B4|=|АB| 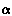 - угол наклона АВ к плоскости Н.
- угол наклона АВ к плоскости Н.
Решение второй задачи: Заменим плоскость Н на Н1
(Н1 V1)
V1)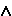 (H1
(H1 [AB])
[AB])  x2
x2 [A4B4]
[A4B4]
Ax2A5=Bx2B5=A1Ax1=B1Bx1
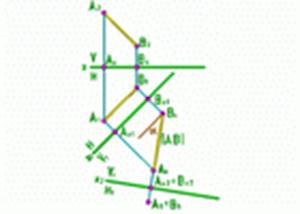 Рис.5
Рис.5
|
Таким преобразованием можно решать задачи об определении истинной величины отрезка и углов наклона его к плоскостям проекций.
Совместное рассмотрение первой и второй задач позволяет решать задачи об определении:
- расстояния от точки до прямой
- расстояния между двумя параллельными прямыми
- расстояния между скрещивающимися прямыми
Третья задача: Заменить плоскость проекций так, чтобы плоскость общего положения стала проецирующей плоскостью.
Четвёртая задача: Заменить плоскость проекций так, чтобы проецирующая плоскость стала плоскостью уровня.
Решим обе задачи совместно:
Решение третьей задачи: Пусть задана плоскость общего положения Р( ABC)
ABC)
Заменим V на V1 (V1 H)
H) (V1
(V1 P) x1
P) x1 [A111]
[A111]
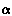 - угол наклона плоскости Р к плоскости Н.
- угол наклона плоскости Р к плоскости Н.
Решение четвёртой задачи: Заменим Н на Н1 (Н1 V1)
V1)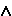 (Н1
(Н1 P) x2
P) x2 [C4B4]
[C4B4]
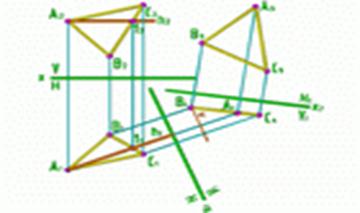 Рис.6
Рис.6
|
С помощью такого преобразования можно решать задачи на определение: углов наклона плоскости к плоскости проекций, расстояния от точки до плоскости, расстояния между параллельными плоскостями.
Совместное решение задач 3 и 4 позволяет решать задачи на определение: натуральных величин плоских фигур, углов между пересекающимися прямыми, расстояния между параллельными прямыми, расстояния от точки до прямой.
| 2. Вращение вокруг прямых уровня. 3. Совмещение - вращение вокруг следа плоскости. | Лекции: 1 2 3 4 5 6 7 8 9 10 11 12 13 |
 2014-02-12
2014-02-12 555
555








