2014-02-12
2150
Верхние пояса стенок корпуса резервуара в результате расчета на прочность имеют сравнительно небольшую толщину, поэтому необходимо проверять их на устойчивость при определенных сочетаниях нагрузок: вес покрытия и стенки с установленным технологическим оборудованием и теплоизоляцией, снеговая и ветровая нагрузки, избыточное давление и вакуум.
Устойчивость оболочек в значительно большей степени, чем у стержневых конструкций, зависит от их формы, условий закрепления, начальных несовершенств, характера нагрузок. Поэтому в практических расчетах рассматривают отдельно устойчивость цилиндрических, конических, сферических и других оболочек.
В частности, условие устойчивости замкнутых круговых цилиндрических оболочек вращения равномерно сжатых параллельно образующим
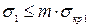, (1.9)
где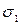 
- расчетное меридиональное напряжение в оболочке; 
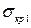- критическое напряжение, равное меньшему из значени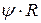й 
и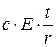 
(r - радиус срединной поверхности, t - толщина оболочки).
Значение коэффициентов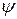 
при 0 <
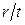< 300 определяют по формуле
|
|
|
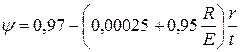. (1.10)
Значения коэффициентов с принимают по табл. 1.1.
Таблица 1.1. Коэффициенты с
|
| |||||||||
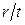| С | 0,22 | 0,18 | 0,16 | 0,14 | 0,11 | 0,09 | 0,08 | 0,07 | 0,06 |
Условие устойчивости замкнутых круговых оболочек вращения при действии равномерного внешнего давления p, нормального к боковой поверхности
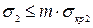, (1.11)
где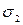 
- расчетное кольцевое напряжение в оболочке; 
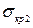- критическое напряжение, определяемое по формулам:
для оболочек коротких и средней длины при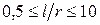 
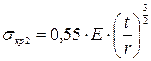; (1.12)
для длинных оболочек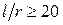 
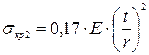; (1.13)
при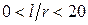 
напряжение 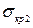определяют линейной интерполяцией (l - длина цилиндрической оболочки).
Если оболочка укреплена достаточно жесткими кольцевыми ребрами, расположенными на расстоянии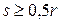 
между их осями, то их поддерживающее влияние учитывается только тем, что длина оболочки принимается равной расстоянию s.
Замкнутую круговую цилиндрическую оболочку, подверженную одновременному действию нагрузок, вызывающих осевое и поперечное сжатие, с небольшим запасом проверяют на устойчивость по формуле
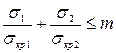. (1.14)
Расчет на устойчивость конической оболочки вращения (см. рис. 1.5) при действии внешнего равномерного давления p, нормального к боковой поверхности, выполняют по формуле (1.11), принимая:
; 
; 
.
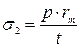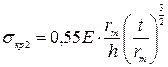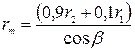Расчет на устойчивость полной сферической оболочки (или ее сегмента) при 
и действии внешнего равномерного давления p, нормального к ее поверхности, следует выполнять по формуле
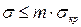, (1.15)
где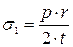 
; 
.
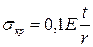Устойчивость стенки незаполненного резервуара проверяется на совместное действие равномерного сжатия вдоль образующих и поперечного сжатия внешним равномерным давлением по формуле
|
|
|
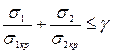, (21.16)
где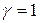 
, а значения 
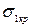и 
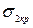определяются по формулам (1.9, 1.10, 1.12, 1.13).
Продольные сжимающие напряжения в стенке возникают от следующих нагрузок:
1) веса крыши и установленного на ней оборудования
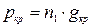, (22.6)
где n1 = 1,1;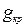 
-принимают в зависимости от объема резервуара:
| Объем резервуара, тыс. м3 | ||||||
| Вес крыши и оборудования, кН/м2 | 0,3 | 0,35 | 0,45 | 0,55 | 0,6 | 0,65 |
2) веса теплоизоляции на крыше
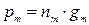, (22.7)
где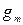 
- вес теплоизоляции, кН/м2, материал и толщина которой назначаются в технологическом задании; 
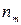=1,2;
3) снега
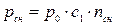(22.8)
где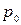 
- вес снегового покрова, кН/м2, принимается для рассматриваемого района строительства по СНиП II-6-74; 
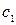= 1; 
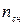=1,4;
4) вакуума
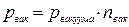(22.9)
где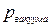 
=0,25 кПа; 
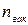=1,2;
5) ветровой нагрузки на боковую поверхность корпуса резервуара, создающей отсос на крыше и вызывающей продольные растягивающие напряжения в стенке резервуара,
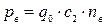(22.10)
где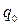 
- нормативный скоростной напор, кН/м2, в зависимости от района строительства, принимаемый по СНиП II-6-74; 
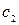= 0,8 - аэродинамический коэффициент для крыши; 
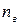=0,8 - коэффициент перегрузки для ветрового отсоса;
6) веса стенки с учетом теплоизоляции на рассматриваемом уровне (низ самого нижнего из наиболее тонких листов стенки)
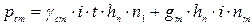(22.11)
где i - число поясов выше рассматриваемого уровня;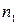 
= 1,1; 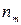=1,2.
Таким образом, суммарные продольные напряжения в стенке от действующих нагрузок равны:
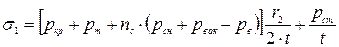(22.12)
где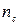 
= 0,9 - коэффициент сочетаний нагрузок.
Кольцевые сжимающие напряжения в стенке возникают от следующих нагрузок:
1) ветровой нагрузки, которая принимается равномерно распределенной по окружности резервуара. Действие ветровой нагрузки на стенку заменяется действием условного вакуума
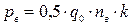, (22.13)
где 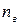=1,2 - коэффициент перегрузки для ветровой нагрузки; 
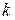- коэффициент, учитывающий изменение скоростного напора по высоте, принимаемой по СНиП II-6-74;
2) вакуума
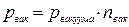(22.14)
где 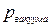=0,25 кПа; 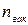=1,2;
Тогда суммарные кольцевые напряжения в стенке от действующих нагрузок равны;
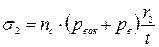(22.15)
где 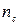=0,9.
Если в результате расчета по условию (21.16) требуется значительно увеличить толщину стенки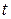 
, то оказывается целесообразным установить промежуточные кольца жесткости (от одного до трех), повышающие критические напряжения .
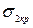В этом случае зоны h' и h" (рис. 22.6) проверяют по формуле (21.16) отдельно при своих значениях tmin,вычисляя 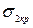при h = h' и h = h" /. Для зоны высотой h' к меридиональным напряжениям 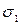добавляют напряжения 
(в верхнем i- мпоясе зоны h') от массы стенки по формуле
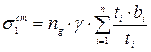(22.16)
где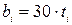 
.
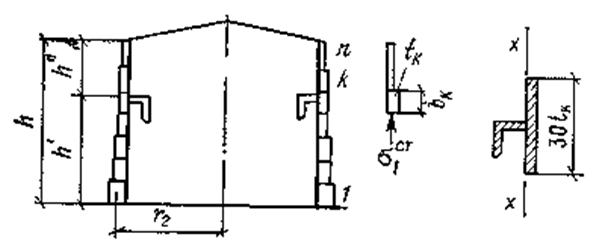
Рис. 22.6. Схема усиления стенки резервуара кольцами жесткости
Критическая сила в кольце должна быть больше действующего в нем усилия от нагрузки, определяемой по формуле (22.15):
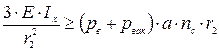(22.17)
где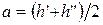 
.
Из условия (22.17) определяют требуемое значение Ix и подбирают соответствующий профиль промежуточного кольца жесткости.
