Расчет сопряжения стенки с днищем

В зоне сопряжения стенки резервуара с днищем за счет стесненности радиальных деформаций стенки днищем возникают изгибающий момент и поперечная сила. Расчетная схема и основная систе­ма сопряжения показаны на рис. 22.7.

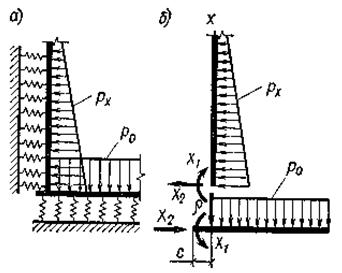
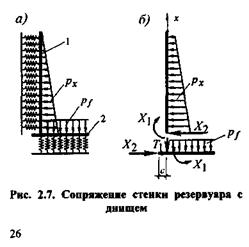
Рис. 22.7. Узел сопряжения стенки резервуара с днищем: а – расчетная схема; б - основная система

Предполагается, что полоски еди­ничной ширины, вырезанные из стенки и днища, работают как балки на упругом основании (по гипотезе Винклера). Основную систему получи­ли путем отрыва стенки от днища. Лишние неизвестные (Х ₁ - изгибаю­щий момент, Х₂ - поперечная сила) определяются методом сил из ре­шения канонических уравнений:

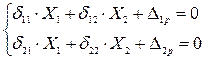(22.18)

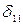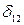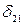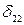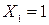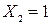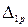где ; =; - единичные перемещения от и ;и 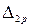- грузовые члены, зависящие от внешних нагрузок, действующих на сопряжение

Все перемещения состоят из двух слагаемых, выражающих соответ­ственно перемещения стенки и днища:

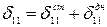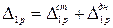; и т. д. (22.19)

Принято, что днище абсолютно жесткое на растяжение и не дефор­мируется в горизонтальной плоскости от действия внешней нагрузки, момента и поперечной силы .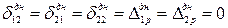

Тогда система уравнений (22.18) принимает вид

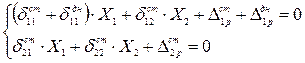(22.20)

Все перемещения, входящие в канонические уравнения, получают из решения диффе­ренциального уравнения оси изогнутой балки на упругом основании

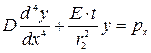(2.12)

Обозначив коэффициент постели стенк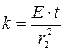и и 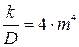, уравнение

(2.12) представляют в виде:

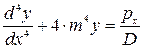(2.13)

где 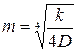- коэффициент деформации стенки; 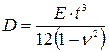- цилиндрическая жесткость стенки; 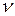- коэффици­ент Пуассона, Е - модуль упругости стали.

Общее решение однородного уравнения (уравнения 2.13 без правой части) имеет вид

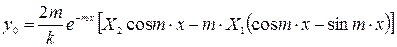. (2.14)

Дифференцируя это уравнение, находим выражение для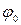

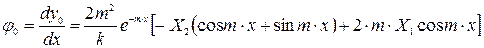. (2.15)

Принимая 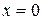, , 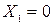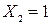из уравнения (2.14) получают

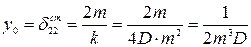(2.16)

Аналогично, при 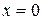, , 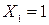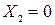из уравнения (2.15) находят

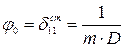(2.17)

и из любого из них

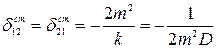(2.18)

Из решения частного неоднородного уравнения определяют перемещения точек стен­ки резервуара от гидростатического давления

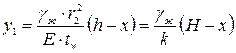(2.19)

Принимая 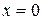,получаем выражение для перемещения стенки

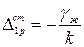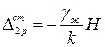; (2.20)

Значения единичных перемещений днища находят, используя теорию изгиба полубес­конечной балки на упругом основании, находящейся под действием сосредоточенного мо­мента, приложенного на расстоянии с от левого конца балки, вертикальной силы, включая собственный вес покрытия и корпуса T ₁, также действующего на расстоянии с от левого конца балки, и гидростатического давления жидкости на уровне днища p₀, начало эпюры ко­торой отстоит от левого конца балки на расстоянии с (х = с):

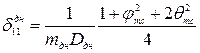(2.21)

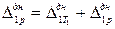(2.22)

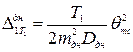
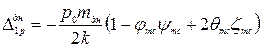(2.23)

Здесь для сокращения записи использованы обозначения:

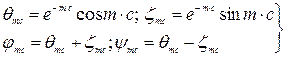(2.24)

где по аналогии со стенкой

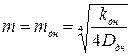, (2.25)

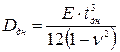. (2.26)

В формулах (2.24 - 2.26) 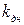- коэффициент постели основания, принимаемый равным от 0,05 до 0,2 кН/см³ в зависимости от степени уплотнения песчаного основания и равным 0,3¸1,5 кН/см³ при наличии железобетонного фундамента; 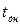- толщина окраек днища, принимаемая равной 0,35¸0,5 толщины листа нижнего пояса стенки; с - величина свеса днища (назначается в пределах от 3 см для резервуаров малого объема, до 8 см для резервуа­ров большой вместимости).

После вычисления перемещений и решения системы канонических уравнений (2.11) определяют неизвестные 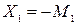и . И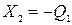згибающий момент в кольцевом направле­нии 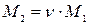; кольцевое усили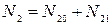е где

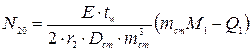(2.27)

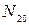- кольцевое усилие моментного напряженного состояния; 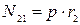- кольцевое уси­лие безмоментного состояния.

Длина полуволны затухания краевого эффекта .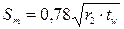

В пределах этого расстояния кольцевые усилия за счет стесненности кольцевых дефор­маций меньше, чем на вышележащих участках стенки. Изгибающий момент в днище

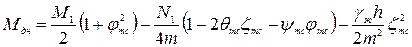(2.28)

Проверка напряжений с учетом краевого эффекта.

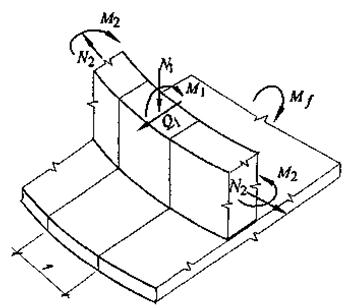
Рис. 2.8. Напряженное состояние стенки в зоне краевого эффекта

Как видно на рис. 2.8, в общем случае условие прочности при действии меридиональ­ных напряжений в стенке

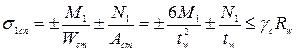(2.28)

Знак перед 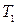зависит от рассматриваемого расчетного случая: ми­нус - при сочетании нагрузок: собственный вес кровли и стенки, снего­вая нагрузка, вакуум; плюс - при сочетании нагрузок: собственный вес кровли и стенки, избыточное давление, ветровой отсос.

Кольцевые напряжения в стенке

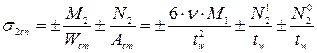(2.29)

Условие прочности 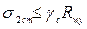. Изгибное напряжение в днище

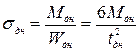(2.30)

Условие прочности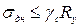

Проверку прочности уг­лового шва, прикрепляюще­го стенку к днищу, произво­дят на одновременное воз­действие поперечной силы и момента. Меридиональ­ное усилие ввиду малости не учитывают. Величину ка­тета шва предварительно за­дают в пределах 0,3 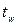. Прочность проверяют по металлу шва и по границе сплавления.

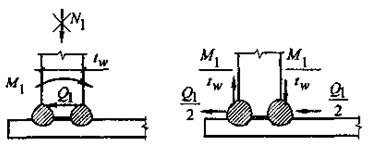
Рис. 2.9. Расчетная схема сварного шва, соединяющего стенку с днищем

Представляя момент 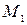как произведе­ние силы на плечо (рис.2.9) и распределяя поперечную силу на два шва, получаем условие прочности по металлу шва

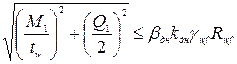(2.32)

и аналогично по границе сплавления.

При пустом резервуаре возможен отрыв корпуса резервуара от осно­вания под действием внутреннего избыточного давления и ветрового воз­действия. Для предупреждения отрыва по периметру резервуара преду­сматривают постановку анкерных устройств.