Функциональные

Структурные

Классификация математических моделей (ММ).

Наглядность ММ.

Устойчивость ММ.

Адекватность ММ.

Точность ММ.

Полнота ММ.

Свойства математических моделей (ММ).

Позволяет отразить в достаточной мере те характеристики и особенности технического объекта (ТО), которые нас интересуют.

Дает возможность обеспечить совпадение реальных данных с данными, полученными с помощью ММ. Обычно здесь выделяют погрешности, возникающие при моделировании: относительная и абсолютная погрешности.

Способность ММ описывать выходные данные с заданной точностью.

Это зависимость выходных данных от точности входных данных.

5) Продуктивность ММ.

Связана с способностью располагать достаточно достоверными исходными данными.

Точность результатов не может быть выше точности исходных данных (Принцип Крылова).

Как правило, модель должна быть легко-читаема и универсальна к другим объектам.

По свойству технического объекта:

1) структурные,

2) функциональные,

3) структурно-функциональные.

Если математическая модель отражает устройство технического объекта и связи между составляющими его элементами, такая математическая модель называется структурной.

- Топологические модели отображают состав технического объекта и связи между его элементами. Их обычно применяют на начальном этапе проектирования.

- Геометрические модели обычно применяются при проектировании различных деталей и машин.

Если же математическая модель отображает происходящие в техническом объекте процессы, в этом случае ее называют функциональной.

а) Алгоритмические (модель – некий алгоритм).

б) Аналитические (обычно описываются в виде точных формул, зависимостей и законов).

По способу получения математические модели делятся:

а) Теоретические (подчиняются различным основным законам).

б) Эмпирические (на опыте).

в) Полуэмпирические (строятся на основе пи-теоремы).

Пи-теорема:

Если мажду n-параметрами, характеризующими изучаемый объект, существует зависимость (информационная, физическая, химическая…), то эту зависимость можно представить в виде 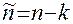- безразмерных операций, где k – число независимых единиц измерения.

Пи-теорема упрощает анализ и позволяет в удобной форме представлять результаты ее качественного исследования.

Пример 1:

Пример 2:

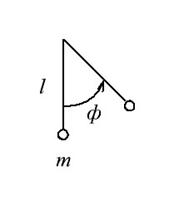
Маятник с невесомой, нерастяжимой нитью.

Если пренебречь сопротивлением воздуха, то в системе устанавливаются незатухающие гармонические колебания.

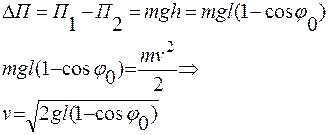
Пусть ставится задача определить период колебаний в зависимости от выбранных параметров системы. В качестве параметров системы выбираем:

В этом случае получаем 5 основных характеристических параметров.

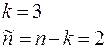
Одной из безразмерных величин необходимо взять угол отклонения математического маятника().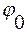

Исключаем массу из рассмотрения, в этом случае 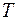не зависит от :

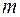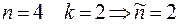
Получим основное соотношение системы через основные параметры:

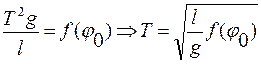
Вычислить функцию 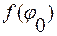, используя данные соотношения невозможно.

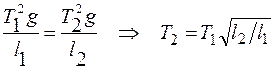
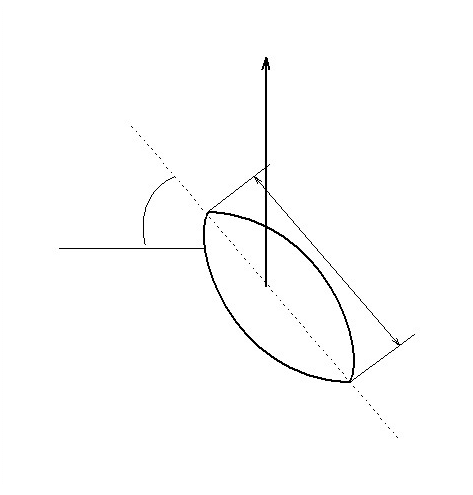
Пример 3:

Математическая модель крыла самолета.

P

		P
	a
		b

Основные параметры системы:

- подъемная сила на единицу длины –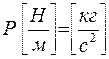

- плотность воздуха –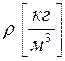

- скорость воздуха –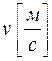

- длина крыла –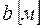

- угол атаки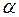

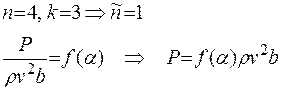
Даная формула позволяет определить подъемную силу крыла по выбранным параметрам системы.

В зависимости от параметров математические модели бывают:

а) Стохастические (параметры – случайные величины)

б) Детерминированные (параметры – определенные величины)

Для стохастических моделей используются методы теории вероятности, а в качестве величин берутся: математические ожидания, дисперсии, законы распределения. В большинстве случаев случайные величины являются либо неизвестными, либо известными с малой точностью, и в этом случае математическая модель не удовлетворяет требованиям продуктивности.

Для детерминированных математических моделей все переменные являются известными, и такая математическая модель всегда продуктивна.

Пример 1

Пусть имеется тело однородное по объему с температурой 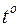, температура окружающей среды – 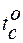, с коэффициентом теплопроводности 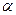, определим как меняется .

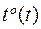Тепловой поток: 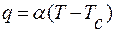(на единицу площади).

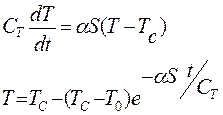Отдаваемая теплота: .

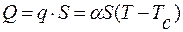Из законов физики известно: 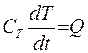, где 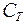- теплоемкость тела.

, где 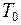– начальное значение температуры тела.

Данная задача является детерминированной, в случае если все коэффициенты модели известны.

Пусть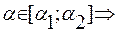

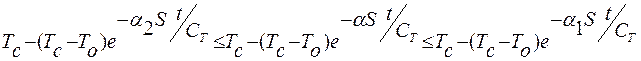
По состоянию во времени математические модели бывают:

- Динамические

- Статические

- Квазистатические

Динамические модели

Внутренние параметры системы зависят от предыстории реакции цепей (описываются дифференциальными уравнениями).

Статические модели

Внутренние параметры системы не зависят от предыстории реакции цепей (описываются алгебраическими уравнениями).

Квазистатические модели

– это такие модели, в которых изменением координат модели можно пренебречь в течении рассматриваемого периода времени.

По линейности:

- Линейные.

- Нелинейные.

По распределению параметров:

- С сосредоточенными параметрами.

- С распределенными параметрами.

По виду внутренних сигналов:

- Непрерывные

- Дискретные

- Смешанные

Тема 2: Математические модели микроуровня.