Область применения, основные положения

Микроуровень (иначе называемый уровнем В) - это уровень проекти­рования базовых элементов. При моделировании на этом уровне фазовые пе­ременные фигурируют как функции нескольких независимых переменных, к которым относятся пространственные координаты и время, причем и про­странство, и время рассматриваются как непрерывные. Математические мо­дели микроуровня отражают процессы, протекающие в общем случае в трех­мерной сплошной среде. Элементами этого уровня являются участки объ­емной структуры, например токоведущая шина в электрических цепях, зубчатое колесо в редукторе, трубка с жидкостью в гидроприводе и т. п.

Типичными фазовыми переменными микроуровня являются плотности электрического тока и магнитного потока, плотности вещества, напряженно­сти полей, концентрации частиц и др.

Внутренними параметрами являются такие величины, как электропро­водность, диэлектрическая и магнитная проницаемость, теплопроводность, концентрация примесей, геометрические размеры элементарных участков, а выходными параметрами — гидравлическое сопротивление участка трубо­провода, электрическое сопротивление резистора, ёмкость конденсатора, магнитная проводимость, жесткость пружины.

Математические модели объектов данного уровня представляют собой дифференциальные уравнения в частных производных. В связи с учетом ха­рактера воздействий и фазовых переменных, распределенных в пространстве, эти модели часто называют распределенными моделями с заданными гра­ничными условиями. Решение дифференциальных уравнений в частных про­изводных представляет значительные вычислительные трудности. Использо­вание распределенных моделей ограничивается случаями объектов с малым числом участков.

Одним из главных принципов создания моделей микроуровня является следующий: при создании теоретических моделей целесообразно исхо­дить из основных физических законов в их наиболее «чистом», фунда­ментальном виде. Соблюдение этого принципа обеспечивает получение достаточно универсальных моделей. В противном случае повышается опас­ность того, что созданная модель окажется несправедливой для ряда условий, причем эти условия могли остаться вне поля зрения пользователя модели.

К наиболее общим фундаментальным законам в первую очередь относятся законы сохранения. Общая формулировка этих законов, может быть записана в следующем виде: изменение во времени некоторой субстанции в элементарном объеме равно сумме притока (стока) этой субстанции через поверхность элементарного объема и скорости генерации (уничтожения) субстанции в рассматриваемом объеме dφ/dt=-divJ+G, где φ — некоторая фазовая переменная, выражающая субстанцию (плотность, энергия, импульс и т. п.); J — поток фазовой переменной; G — скорость генерации субстанции.

Поток фазовой переменной есть вектор J. Дивергенция этого вектора определяется формулой .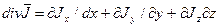

Простейшим примером уравнений сохранения является уравнение 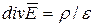, описывающее электростатическое поле. В декартовой системе координат это уравнение более известно как уравнение Пуассона 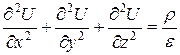. Здесь ρ - плотность электрического заряда; ε - диэлектрическая проницаемость среды, U – электрический потенциал.

Примером из теплотехники может быть нагрев проводника протекающим по нему током. В каждой точке пространства генерируется тепло мощностью 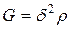, где 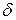- плотность тока, 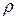- удельное сопротивление материала. Часть тепловой энергии отдаётся соседним точкам 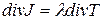, где 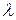- коэффициент теплопроводности, 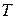- температура. Оставшаяся часть тепла идёт на нагрев 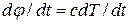, где 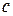- удельная теплоёмкость материала.

§2.1 Сеточные методы расчёта.

Сетки и шаблоны. Решение дифференциальных или интегро-дифференциальных уравнений с частными производными, как правило, выполняется численными методами. Эти методы основаны на дискретизации независимых переменных - их представлении конечным множеством значений в выбранных узловых точках исследуемого пространства. Эти точки рассматриваются как узлы некоторой сетки, поэтому используемые в моделировании методы — это сеточные методы. Сетка может быть триангуляционная или декартова.

Среди сеточных методов наибольшее распространение получили два метода: метод конечных разностей (МКР) и метод конечных элементов (МКЭ). Обычно выполняют дискретизацию пространственных независимых переменных, т. е. используют пространственную сетку. В этом случае результатом дискретизации является СОДУ для задачи нестационарной или система алгебраических уравнений для стационарной.

Под шаблонами понимают формализованный (без вывода) переход от дифференциальных уравнений к конечным разностям. Примеры шаблонов для одномерных и двумерных задач приведены ниже. Здесь кружком большего диаметра обозначены точки, в которых аппроксимируется производная. Черными точками обозначены точки, значения фазовой переменной в которых входят в аппроксимирующее выражение. Число, записанное около узла, равно коэффициенту, с которым значение фазовой переменной входит в аппроксимирующее выражение.

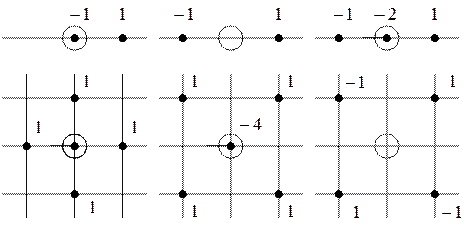
Метод конечных разностей. Рассмотрим пример расчета поля между двумя достаточно длинными проводниками А и В, имеющими разность потенциалов .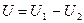

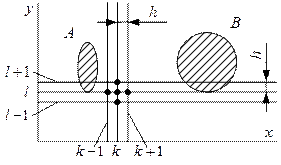Наложим на исследуемое поле сетку с шагом 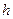. Выберем шаблон, с помощью которого по значениям потенциалов в точках (x,y) c координатами {(k-1)h,lh}, {(k+1)h,lh}, {kh,(l-1)h}, {kh,(l+1)h} и {kh,lh} определяется сумма вторых производных в точке с координатами {kh,lh}: .

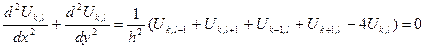Запишем систему уравнений для всех точек исследуемого пространства между проводниками. Решив её, например методом последовательных приближений, находим искомое распределение потенциалов электростатического поля.

Метод конечных элементов основан на аппроксимации не производных, а самого решения 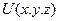. При этом каждый элементарный участок пространства представляется в виде набора элементов с сосредоточенными параметрами. Например, это могут быть элементы сопротивления фазовому потоку при воздействии фазовой силы. Значения сопротивлений могут быть чётко увязаны с неоднородностью и анизотропностью среды.

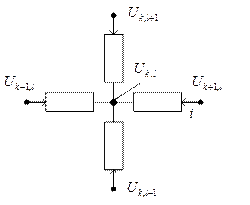
Обратимся к рисунку плоскопараллельного поля, рассмотренного ранее. Пусть в точках пространственной сетки c координатами {(k-1)h,lh}, {(k+1)h,lh}, {kh,(l-1)h}, {kh,(l+1)h} и {kh,lh} потенциалы поля имеют значения 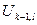, , 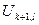, 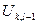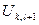и 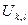. Между точками включены сопротивления, как показано на рисунке. Значение сопротивления участка равно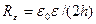

В связи с тем, что зарядов в исследуемом объёме пространства нет, то сумма фазовых потоков (у нас это поток электростатической индукции 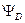) равна нулю, или

.

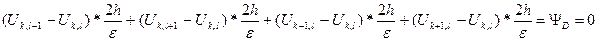Примечание: уравнение применимо пр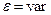и и .

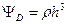Составляя уравнения для каждой точки сетки и решая полученную систему линейных уравнений, находим искомое распределение потенциалов.

Указанным методом удобно решать изложенную выше задачу теплового поля.

Примечания. Выведенные выше уравнения модели поля имеют дифференциальный вид. При переходе к сеточным методам уравнения необходимо корректировать применительно к интегральной форме (с учётом шага сетки).

Тема 3: Модели макроуровня