Идеальные гидравлические (пневматические) двухполюсники

В качестве потенциальной фазовой переменной гидравлической подсистемы принимается давление Р, в качестве потоковой фазовой переменной - массовый расход в единицу времени .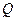

Гидравлическое сопротивление. Из курса физики известно, что для достаточно длинного трубопровода при ламинарном движении жидкости её расход пропорционален разности давлений на концах трубопровода. В частности, для цилиндрического трубопровода расход определяется по формуле 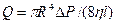. Принимая величину 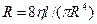как гидравлическое сопротивление трубопровода, получаем математическую модель ламинарного движения жидкости 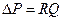. Здесь 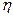- кинематическая вязкость, R и l –радиус и длина трубопровода.

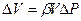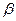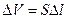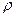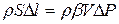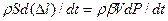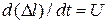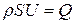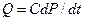Гидравлическая ёмкость (сжимаемость жидкости). Уравнение сжимаемости жидкости в некотором объеме V при воздействии давления Р определяется как ., где - коэффициент сжимаемости жидкости, . Умножим обе части уравнения на плотность : . Продифференцируем уравнение по времени . Так как - скорость движения жидкости, то и , где 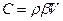- аналог электрической емкости.

Гидравлическая индуктивность (инерционность жидкости). Рассмотрим участок трубопровода длиной l с давлениями на концах 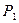и 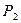. В соответствии с уравнением Эйлера (закон движения идеальной – несжимаемой жидкости) 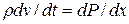, где 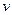- скорость движения жидкости. Полагая скорость изменения давления постоянной по всей длине трубопровода, переходя от производной к конечным разностям, перепишем уравнение к виду 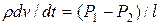. Для получения в левой части уравнения массового расхода умножим обе его части на 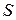, т. е. 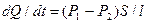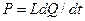, или , где 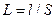- аналог электрической индуктивности.

Закон движения реальной жидкости описывается уравнением Навье - Стокса, которое для одномерного случая, выглядит как 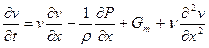, где 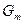- генерируемые массовые силы; 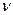- вторая вязкость. Выделяя участок трубопровода, считая 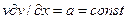, получим, что участок может быть представлен гидравлическими сопротивлением и индуктивностью (массовыми силами пренебрегаем), т. 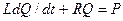е. , где .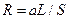

§3.3. Идеальные четырёхполюсники