Дополнение евклидова пространства

Рассмотрим следующие примеры центрального проецирования.

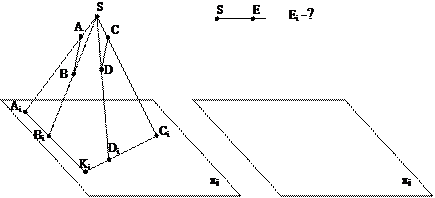Т.к. 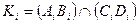, то по смыслу операции должна существовать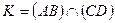, но такой точки нет, т.к. (AB)║(CD). Возникает нарушение соответствия, устанавливаемого проецированием между оригиналом и проекцией. Рассмотрим меры по устранению такого несоответствия.

Операцию центрального проецирования мы рассматриваем в евклидовом геометрическом пространстве. В евклидовом пространстве параллельные прямые не пересекаются. Условимся считать параллельные прямые пересекающимися в бесконечно удаленной (несобственной) точке. Каждая прямая дополняется несобственной точкой, к каждая точка дополняется несобственной прямой. Их совокупность порождает несобственную плоскость. Пространство, дополненное несобственными элементами – точками, прямыми и плоскостью – называется расширенным евклидовом пространством. Таким образом, дополнение евклидова пространства приводит к тому, что восстанавливается соответствие между точками оригинала и их проекциями.

В связи с тем, что каждая точка пространства при заданном аппарате проецирование будет иметь одну и только одну проекцию, но обратное утверждение не имеет место. Для определения положение точки в пространстве, необходимо иметь две ее центральные (или параллельные) проекции, полученные при двух различных центрах (или направлениях) проецирования.

Ортогональное проецирование обладает рядом преимуществ перед центральным и параллельным косоугольным проецированием. К ним в первую очередь следует отнести:

1. простоту геометрических построений для определения ортогональных проекций точек;

2. возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры.

Два важных свойства ортогональной проекции:

· проекции взаимно параллельных прямых также взаимно параллельны, а отношение отрезков таки прямых равно отношению их параллельных проекций;

· для того, чтобы прямой угол проецировался ортогонально без искажения, необходимо и достаточно, чтобы, по крайне мере, одна его сторона была параллельна плоскости проекции, а вторая сторона – не перпендикулярна этой плоскости.