Проекции точки

Ортогональной проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на эту плоскость. Координатами называют числа, которые ставят в соответствии точке для определения ее положения в пространстве или на поверхности.

В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x, y, z. X – абсцисса, y – ордината, z – аппликата. Абсцисса x определяет расстояние от данной точки до плоскости p­₃, ордината y - до плоскости p­₂, аппликата z - до плоскости p­₁.

Какая-либо точка пространства A, заданная координатами, будет обозначаться так: A (x, y, z). Построение изображения самой точки и ее проекций на пространственной модели рекомендуется осуществлять с помощью координатного прямоугольного параллелепипеда. Прежде всего на осях координат от точки O откладывают отрезки, соответственно равные единицам длины. На этих отрезках (OA_X, OA_Y, OA_Z), как на ребрах, строят прямоугольный параллелепипед. Вершина его, противоположная началу координат, и будет определять заданную точку A.

Построение параллелепипеда позволяет определить не только точку A, но и все три ее ортогональные проекции.

Лучами, проецирующими точку на плоскости П₁, П₂ и П₃, являются те три ребра параллелепипеда, которые пересекаются в точке A.

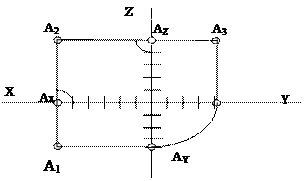Каждая из ортогональных проекций точки A, будучи расположенной на плоскости, определяется только двумя координатами. Так, горизонтальная проекция A₁ определяется координатами x и y, фронтальная проекция A₂ - координатами x и z, профильная проекция A₃ - координатами y и z. Но две любые проекции определяются тремя координатами. Вот почему задание точки двумя проекциями равносильно заданию точки тремя координатами.

На эпюре где все плоскости проекций совмещены, проекции A₁ и A₂ окажутся на одном перпендикуляре к оси OX, а проекции A₂ и A₃ - на одном перпендикуляре к оси OZ.

Что касается проекций A₁ и A₃, то и они связаны прямыми A₁A_y и A₃A_y, перпендикулярными оси OY. Но так как эта ось на эпюре занимает два положения, то отрезок A₁A_y не может быть продолжением отрезка A₃A_y.

Построение проекций точки A на эпюре по заданным координатам выполняют в такой последовательности: прежде всего на оси абсцисс от начала координат откладывают отрезок OA_X = x, а затем через точку A_X проводят перпендикуляр к оси Ox, на котором с учетом знаков откладываем отрезки A_XA₁ = y (получаем A₁) и A_XA₂ = z ((получаем A₂). Остается построить профильную проекцию точки A₃. Так как профильная и фронтальная проекции точки должны быть расположены на одном перпендикуляре к оси Oz, то через A₂ проводят прямую A₂A_Z ^Oz.

Наконец, возникает последний вопрос: на каком расстоянии от оси Oz должна находиться A₃? Рассматривая координатный параллелепипед, ребра которого A_ZA₃ = OA_Y = A_XA₁ = y, заключаем, что искомое расстояние A_ZA₃ равно y. Отрезок A_ZA₃ откладывают вправо от оси Oz, если y > 0, и влево, если y < 0.