Решение
Пример 5.1.4
Решим пример 5.1.1. методом Сэвиджа.
Найдем в матрице риска максимальный элемент в каждой строке (табл. 5.1.5).
Таблица 5.1.5
| матрица рисков | макс в строке | |||||
| ГКО | ||||||
| ГФ | 6,5 | |||||
| Проект 1 | ||||||
| Проект 2 | ||||||
| min max |
По критерию Сэвиджа видно, что инвестору выгодно принять Проект 2.
Изучаемые вопросы:
Ø Ожидаемая доходность финансовой операции.
Ø Ожидаемый риск финансовой операции.
Принятие решений по правилу Вальда и правилу Сэвиджа дают гарантированные оценки доходности финансовых операций. Эти оценки можно улучшить, если использовать информацию о состоянии экономики. В первую очередь о вероятности того или иного состояния экономики. Финансовая операция называется вероятностной, если можно оценить вероятность каждого ее исхода.
Пусть финансовая операция допускает n различных исходов. Обозначим dj случайную доходность операции, а pj – ее вероятность.
Финансовая операция является дискретной случайной величиной x с рядом распределения
| x | d 1 | … | dn |
| pj | p 1 | … | pn |
Ожидаемой доходностью или эффективностью финансовой операции называется математическое ожидание ее случайной доходности x
m = d 1 p 1 + d 2 p 2 +... + dn pn.
Дисперсией финансовой операции называется дисперсия ее случайной доходности x.
D = M (x 2) – m 2.
Рискомфинансовой операции r называется среднеквадратичное отклонение ее случайной доходности x
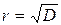 .
.
 2014-02-12
2014-02-12 384
384








