Свойства гармонических полей

В случае, когда функции u и v являются гармоническими, формулы Грина примут следующий вид:

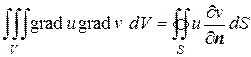. (8.51)

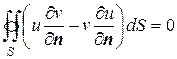. (8.52)

Из формул Грина можно вывести следующие свойства гармонических функций.

1⁰. Если v – функция, гармоническая в некоторой области V, ограниченной поверхностью S, то

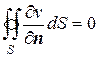, (8.53)

где S – любая замкнутая поверхность, целиком лежащая в области V.

Это свойство гармонических функций можно интерпретировать как условие отсутствия источников внутри области V.

2⁰ (теорема о среднем). Если v – функция, гармоническая в некоторой области V, а M какая-либо точка, лежащая внутри области V, то имеет место формула

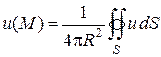, (8.54)

где S – сфера радиуса R с центром в точке M, целиком лежащая в области V.

Это теорема утверждает, что значение гармонической функции в некоторой точке M равно среднему значению этой функции на любой сфере S с центром в точке M, если сфера не выходи за пределы гармоничности функции u.

Замечание. Отметим, что формулу (8.54) можно записать также в виде

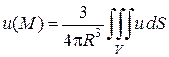. (8.55)

3⁰ (принцип максимального значения). Если функция v, определенная и непрерывная в замкнутой области V, удовлетворяет уравнению Лапласа внутри V, то максимальное и минимальное значения функции u достигаются на поверхности S.