Для расчета перечисленных характеристик одномерных фильтрационных потоков жидкости и газа можно использовать два подхода. Первый из них – вывод дифференциальных уравнений и их решение отдельно для прямолинейно-параллельного, плоскорадиального и радиально-сферического потоков жидкости и газа. Второй – вывод обобщенного уравнения одномерного течения флюида в недеформируемой трубке тока переменного сечения с использованием функции Лейбензона и получение из него конкретных формул применительно к различным схемам фильтрационных потоков. Второй подход более эффективен, позволяет исходить из обобщенных характеристик течения, он был использован и при выводе следующих характеристик:
Прямолинейно – параллельная фильтрация несжимаемой жидкости
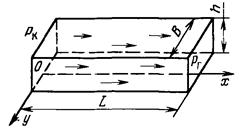 Схема прямолинейно-параллельного одномерного течения несжимаемой однородной ньютоновской жидкости в изотропном недеформируемом пласте (рис.). Пусть пласт представляет собой прямоугольный параллелепипед, шириной В и толщиной h, ограниченный сверху снизу непроницаемыми плоскостями, слева контуром питания, справа – галереей.
Схема прямолинейно-параллельного одномерного течения несжимаемой однородной ньютоновской жидкости в изотропном недеформируемом пласте (рис.). Пусть пласт представляет собой прямоугольный параллелепипед, шириной В и толщиной h, ограниченный сверху снизу непроницаемыми плоскостями, слева контуром питания, справа – галереей.
|
|
|
Площадь поперечного сечения 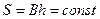 ; на контуре питания x1 = 0, р1 = рK, на галерее x2 = L, р2 = рГ.
; на контуре питания x1 = 0, р1 = рK, на галерее x2 = L, р2 = рГ.
рK – значение давления на контуре питания, рГ - на галерее.
Название контур питания обусловлено тем, что через плоскость х = 0 происходит приток в пласт жидкости, которая далее фильтруется к галерее x = L. Ось х направляем параллельно вектору скорости фильтрации.
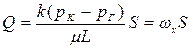 , (3.1)
, (3.1)
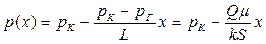 ,
, 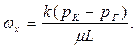 (3.2, 3.3)
(3.2, 3.3)
Давление в пласте при прямолинейно-параллельной фильтрации распределено по линейному закону, а скорость фильтрации во всем пласте постоянна.
При определении фильтрационных характеристик пласта по методу установившихся отборов строится индикаторная линия, которая представляет график зависимости расхода от разности давлений на контуре питания и галерее. Эта разность называется депрессией на пласт. Таким образом, индикаторная линия представляет собой график зависимости вида 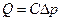 ,
,
где С – коэффициент продуктивности. 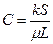 .
.
Следовательно, при выполнении закона Дарси индикаторная линия представляется в виде прямой линии.
Еще одна промысловая задача связана с определением времени движения в пласте «меченых частиц». Для этого в фильтрационный поток добавляют изотопы некоторых атомов или другие частицы, которые можно идентифицировать с помощью специальных методов. Время движения «меченых частиц» определяется из закона движения с помощью определения истинной средней скорости.
Если пористоть равна просветности, то время, за которое «меченая частица» переместиться от контура питания до произвольной точке в пласте
|
|
|
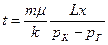 (3.4)
(3.4)
Время, за которое «меченая частица» переместиться от контура питания до галереи или время прохождения всего пласта
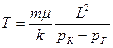 (3.5)
(3.5)
где m – пористость, k – проницаемость пористостых сред.
Если пористоть не равна просветности, то вводится структурный коэффициент 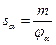 , φα – в однородно пористой среде константа.
, φα – в однородно пористой среде константа.
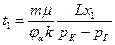 (3.6)
(3.6)
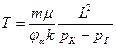 (3.7)
(3.7)
Учет структурного коэффициента приводит к уменьшению времени движения меченных частиц, т.к. 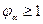 .
.
Еще одной важной характеристикой является средневзвешенное по объему порового пространства пластовое давление 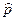 .
.
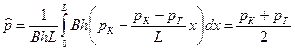 (3.8)
(3.8)
Таким образом, основные фильтрационные характеристики при прямолинейно-параллельной фильтрации несжимаемой жидкости определяются формулами (3.2, 3, 4, 6, 8)
 Плоскорадиальная фильтрация несжимаемой жидкости
Плоскорадиальная фильтрация несжимаемой жидкости
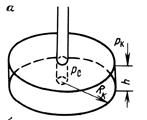
Схема плоскорадиального потока в круговом пласте.
Пусть имеем в круговом пласте толщиной h и радиуса Rк центральную скважину радиуса rc, на забое которой поддерживается постоянное давление. На боковой поверхности r = Rк также поддерживается постоянное давление рк (рк > pс) и через нее происходит приток флюида, равный дебиту скважины. Поэтому фильтрация установившаяся, а боковая поверхность, через которую происходит приток, называется контуром питания.
От координаты S переходим к r, отсчитываемой от центра скважины. Для добывающей скважины 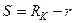 ,
, 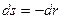 , площадь фильтрационной поверхности
, площадь фильтрационной поверхности 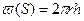 - боковая поверхность цилиндра; на контуре питания r 1 = R k, р2 = рK на забое скважины r2 = rc, р2 = рC.
- боковая поверхность цилиндра; на контуре питания r 1 = R k, р2 = рK на забое скважины r2 = rc, р2 = рC.
Выражение для дебита (объемного расхода) скважины
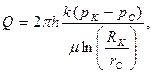 (3.9)
(3.9)
Равенство (3.9) называется формулой Дюпюи, по имени французского инженера-гидравлика XIX века.
Формулы для распределения давления в пласте
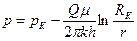 ,
, 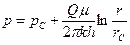 (3.10)
(3.10)
Или используя формулу Дюпюи равенства (3.10) можно привести к виду
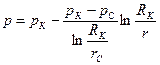 ,
, 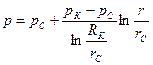 (3.11)
(3.11)
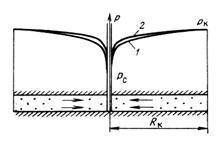 Формулы (3.10, 3.11) эквивалентны, из них следует, что давление в пласте распределено по логарифмическому закону. Поэтому при значениях радиуса, близких к контуру питания, значения давления изменяются не значительно, но при приближении к скважине давление резко изменяется (рис. 3.5, на рис. кривые распределения в плоскорадиальном потоке: 1 – для жидкости, 2 – для газа). Формулы (3.10, 3.11) в пространстве и определяют поверхности, которые получаются вращением образующей вокруг оси симметрии скважины. Поверхность, соответствующая распределению давления, носит название воронки депрессии. Аналогично ведет себя и градиент давления и скорость фильтрации (с той лишь разницей, что давление при приближении к скважине резко уменьшается, а скорость возрастает).
Формулы (3.10, 3.11) эквивалентны, из них следует, что давление в пласте распределено по логарифмическому закону. Поэтому при значениях радиуса, близких к контуру питания, значения давления изменяются не значительно, но при приближении к скважине давление резко изменяется (рис. 3.5, на рис. кривые распределения в плоскорадиальном потоке: 1 – для жидкости, 2 – для газа). Формулы (3.10, 3.11) в пространстве и определяют поверхности, которые получаются вращением образующей вокруг оси симметрии скважины. Поверхность, соответствующая распределению давления, носит название воронки депрессии. Аналогично ведет себя и градиент давления и скорость фильтрации (с той лишь разницей, что давление при приближении к скважине резко уменьшается, а скорость возрастает).
Проанализируем полученные соотношения для плоскорадиальной фильтрации. Для несжимаемой жидкости давление меняется вдоль координаты r по логарифмическому закону (рис. 3.8, кривая 1). Вращение кривой р (r) в пространстве вокруг оси скважины образует поверхность, называемую воронкой депрессии. В точке r = Rk - на контуре питания - кривая не касается горизонтальной линии, а пересекает ее под некоторым углом. Воронка депрессии вследствие логарифмического закона распределения давления имеет большую кривизну вблизи скважины. Следовательно, основная часть депрессии на пласт (рk - рс) сосредоточена в призабойной зоне скважины, параметры которой сильно влияют на дебит скважины. Давление одинаково в тех точках пласта, в которых r = const или, в декартовых координатах х 2 + у 2 = r 2 = const. Это означает, что изобарами (линиями равного давления) являются окружности, концентричные оси скважины. Траектории частиц - радиальные прямые - вместе с изобарами образуют фильтрационное поле течения к скважине. Семейства линий тока (траекторий) и изобар всегда ортогональны друг другу. Сравнение кривых распределения давления в круговом пласте для несжимаемой жидкости и газа при одинаковых граничных условиях показывает, что в газовом потоке имеет место более резкое падение давления вблизи скважины и весьма малое вдали от нее, так что кривая р (r) для газа располагается выше, чем для жидкости (см. рис. 3.8, кривая 2).
|
|
|
Скорость фильтрации определяется
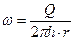 (3.12)
(3.12)
 Через любую цилиндрическую поверхность, концентрично расположенную относительно скважины, в единицу времени протекает один и тот же объем несжимаемой жидкости (Q = const). Поэтому вблизи контура питания площадь боковой поверхности цилиндра очень велика и скорости малы. При приближении скважине площадь поверхности постоянно уменьшается, и скорость возрастает (рис. 3.6). Для того чтобы скорость возрастала, необходимо увеличить градиент давления.
Через любую цилиндрическую поверхность, концентрично расположенную относительно скважины, в единицу времени протекает один и тот же объем несжимаемой жидкости (Q = const). Поэтому вблизи контура питания площадь боковой поверхности цилиндра очень велика и скорости малы. При приближении скважине площадь поверхности постоянно уменьшается, и скорость возрастает (рис. 3.6). Для того чтобы скорость возрастала, необходимо увеличить градиент давления.
 Уравнение индикаторной линии при плоскорадиальном потоке, также как и в случае фильтрации в галерее, задается уравнением прямой (рис. 3.7)
Уравнение индикаторной линии при плоскорадиальном потоке, также как и в случае фильтрации в галерее, задается уравнением прямой (рис. 3.7)
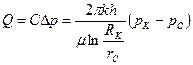 (3.13)
(3.13)
с коэффициентом продуктивности 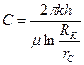 .
.
Вид индикаторной линии не зависит от геометрии потока и определяется только законом фильтрации. Отношение массового дебита скважины Q m к перепаду давления D р называется коэффициентом продуктивности скважины С.
Из (3.13) для жидкости 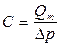 или
или 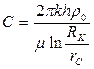
Коэффициент продуктивности определяется в результате исследования скважины при установившихся отборах. Если исследования скважины выполнены при 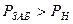 (
(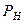 - давление насыщения нефти газом), то по тангенсу угла наклона коэффициент продуктивности скважины
- давление насыщения нефти газом), то по тангенсу угла наклона коэффициент продуктивности скважины
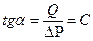 ,
, 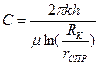 ,
,
где 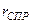 - приведенный радиус скважины.
- приведенный радиус скважины.
Приведенный радиус скважины – это радиус гидродинамически совершенной скважины, которая обеспечивает при равных прочих условиях такой же дебит, как гидродинамически несовершенная скважина, 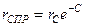 .
.
Расчетные соотношения для определения времени движения «меченой частицы» в плоскорадиальном потоке.
Если пористость равна просветности время движения «меченой частицы» от контура питания до произвольной точки пласта
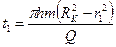 или используя формулу Дюпюи
или используя формулу Дюпюи 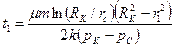 (3.14)
(3.14)
Из (3.14) следует, что «меченая частица» пройдет расстояние от контура питания до скважины за время Т
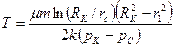 или rC/RK <<1 то
или rC/RK <<1 то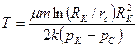 (3.15)
(3.15)
Если пористость неравна просветности, то появляется структурный коэффициент
|
|
|
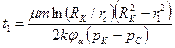 ,
, 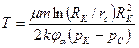 (3.16)
(3.16)
Средневзвешенное по поровому пространству давление при RK/rC >> 1
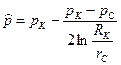 (3.17)
(3.17)
Радиально – сферическая фильтрация несжимаемой жидкости
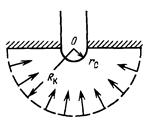 Определим распределение давления и скорости фильтрации в изотропном недеформируемом пласте несжимаемой жидкости. Пусть имеется скважина радиуса rC, вскрывшую кровлю пласта, на забое которой поддерживается постоянное давление рС. Предположим, что толщина пласта h достаточно большая и можно выделить полусферу радиуса RК на поверхности, которой поддерживается постоянное давление рК и через нее проходит поток флюида, равный дебиту скважины. Течение установившееся, поверхность полусферы представляет собой контур питания. Тогда можно предположить, что вскрытие кровли пласта имеет форму полусферы и вектор скорости фильтрации в любой точке пласта между контуром питания и забоем скважины направлен к центру сферы. В этом случае задача имеет сферическую симметрию и ее удобнее решать в сферической системе координат.
Определим распределение давления и скорости фильтрации в изотропном недеформируемом пласте несжимаемой жидкости. Пусть имеется скважина радиуса rC, вскрывшую кровлю пласта, на забое которой поддерживается постоянное давление рС. Предположим, что толщина пласта h достаточно большая и можно выделить полусферу радиуса RК на поверхности, которой поддерживается постоянное давление рК и через нее проходит поток флюида, равный дебиту скважины. Течение установившееся, поверхность полусферы представляет собой контур питания. Тогда можно предположить, что вскрытие кровли пласта имеет форму полусферы и вектор скорости фильтрации в любой точке пласта между контуром питания и забоем скважины направлен к центру сферы. В этом случае задача имеет сферическую симметрию и ее удобнее решать в сферической системе координат.
В этом случае для добывающей скважины с полусферическим забоем имеем: 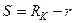 ,
, 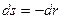 ,
, 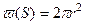 - площадь поверхности полусферы с радиусом r, r 1 = R k, P1 = PK, r 2 = r C, P2 = PC.
- площадь поверхности полусферы с радиусом r, r 1 = R k, P1 = PK, r 2 = r C, P2 = PC.
Формула распределения давления примет вид
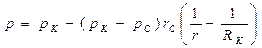 (3.18)
(3.18)
Формула для расчета дебита
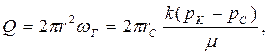 (3.19)
(3.19)
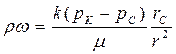 .
.
 2014-02-12
2014-02-12 9024
9024








