Доказательство.
Следствие. Если элемент a имеет симметричный элемент а’ относительно ассоциативной операции 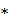 , то все левые и все правые симметричные к а элементы совпадают с элементом а’.
, то все левые и все правые симметричные к а элементы совпадают с элементом а’.
Наиболее часто используется аддитивная и мультипликативная формы записи бинарной операции. При аддитивной форме записи бинарную операцию 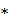 называют сложением и пишут а + b вместо a
называют сложением и пишут а + b вместо a 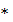 b, называя элемент a + b суммой a и b. Элемент, симметричный элементу а, обозначают (- а) и называют противоположным элементу а. Нейтральный элемент относительно сложения обозначают символом 0 и называют нулевым элементом относительно сложения. При аддитивной записи свойства ассоциативности и коммутативности записывается в виде
b, называя элемент a + b суммой a и b. Элемент, симметричный элементу а, обозначают (- а) и называют противоположным элементу а. Нейтральный элемент относительно сложения обозначают символом 0 и называют нулевым элементом относительно сложения. При аддитивной записи свойства ассоциативности и коммутативности записывается в виде
a + (b + c) = (a + b) + c, a + b = b + a.
При мультипликативной форме записи бинарную операцию называют умножением и пишут a 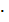 b (вместо а
b (вместо а 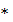 b), называется элемент a
b), называется элемент a 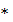 b произведением а и b. Элемент, симметричный а, обозначают а-1 и называют обратным элементу а. Нейтральный элемент относительно умножения обозначают через e и 1 и называют единичным элементом или единицей относительно умножения. При мультипликативной записи свойства ассоциативности и коммутативности записываются в виде a
b произведением а и b. Элемент, симметричный а, обозначают а-1 и называют обратным элементу а. Нейтральный элемент относительно умножения обозначают через e и 1 и называют единичным элементом или единицей относительно умножения. При мультипликативной записи свойства ассоциативности и коммутативности записываются в виде a 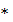 (b
(b 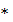 c)=(a
c)=(a 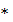 b)
b) 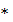 c, a
c, a 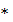 b = b
b = b 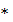 a.
a.
Свойство дистрибутивности умножения относительно сложения записываются в виде (a + b) 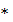 c = a
c = a 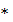 c + b
c + b 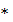 c, c
c, c 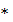 (a + b) = c
(a + b) = c 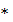 a + c
a + c 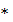 b.
b.
 2014-02-12
2014-02-12 2403
2403
