Моделирование физических процессов в приближении сплошной среды

Моделирование движения заряженных частиц.

Из курса физики учащимся знаком закон Кулона, описывающий взаимодействие точных зарядов. Он похож на закон всемирного тяготения, но роль масс играют заряды.

Наиболее простые модели в данном разделе получаются при моделировании движения одного заряженного тела в поле, созда­ваемом другим заряженным телом («неподвижным», находящем­ся в начале выбранной системы координат). В этой ситуации урав­нения модели практически совпадают с уравнениями движения небесного тела — с точностью до обозначений. Рассматривать бо­лее сложную ситуацию, когда несколько зарядов движутся отно­сительно друг друга, методически нецелесообразно.

Если рассматривать систему из двух зарядов противоположных знаков, то ситуация полностью аналогична задаче двух тяготею­щих тел, обсуждавшейся выше. Если же рассмотреть движение за­ряда, одноименного по знаку с тем, который находится в начале координат, то в соответствующих уравнениях просто сменятся знаки; однако траектории движения будут совсем непохожи на траектории движения в случае разноименных зарядов. Соответ­ствующее моделирование вполне посильно учащимся, особенно если эта тема следует за моделированием движения небесных тел. После проведения простых численных экспериментов по мо­делированию движения заряженного тела можно перейти к более сложным проектам исследовательского характера. Задания для та­ких проектов можно найти, в частности, в задачнике [5].

Целью этих занятий является как углубление навыков моде­лирования физических процессов, так и выработка реального пони­мания понятия «сплошная среда», столь важного в физическом мире. Кроме того, возникает возможность еще раз продемонстрировать в работе прием дискретизации, фундаментальный для информатики.

План занятий по этой теме может быть следующим. Вначале проведите лекцию на тему, что отражает абстрактное понятие «сплошная среда». Физические примеры — жидкости, газы; близкие примеры из самой информатики — графическая информация; звуковая информация и т.д. Напомните учащимся, что при описании явлений, проистекающих в сплошной среде, свойства объекта описываются с помощью непрерывных величин (функций). Примеры, которые здесь уместны, связаны с диффузией, теплопроводностью, потоками жидкости и газа, распространением электромагнитных волн и др.

На этой же лекции уместно рассмотреть вопрос о роли научной графики в компьютерном моделировании. Так, при моделировании процесса теплопроводности стоит задача наиболее наглядно показать динамику изменения температуры. При этом умести прибегнуть к условной раскраске или условному контрастированию — мощному приему научной графики. Он находит широчайшее применение и представляет собой набор приемов по максимально удобной, хотя и условной, визуализации результатов компьютерного моделирования.

Например, в различных исследованиях температурных полей возникает проблема наглядного представления результатов. Самый простой (и весьма неэффективный) — привести карту (чертеж план), в некоторых точках которой обозначены значения темпе­ратуры. Другой способ — набор изотерм — гораздо эффективнее. Можно добиться еще большей наглядности, учитывая, что боль­шинству людей свойственно, сравнивая разные цвета, восприни­мать красный как «горячий», голубой как «холодный», а все ос­тальные — между ними. Наглядность достигается окрашиванием самого «горячего» участка в ярко-красный цвет, самого «холод­ного» — в ярко-голубой, а остальных — в промежуточные цвета. Получится наглядная картина температурного поля.

А что делать, если дисплей монохромный? Или если изобра­жение нужно перенести с цветного дисплея на бумагу при отсут­ствии возможности цветной печати? Тогда роль цвета может сыг­рать контраст. Сделаем самый «горячий» участок самым темным, самый «холодный» — прозрачным, а остальные — между ними. Эффектность, конечно, меньше, чем при цветовой раскраске, но определенная наглядность достигается.

То же самое можно делать и при иллюстрации температурного поля на поверхности, обрабатываемой на станке детали, и поля температур, полученного путем радиолокации поверхности дале­кой планеты, и во множестве других задач.

Для конкретного моделирования явлений в приближении сплошной среды следует отобрать максимально простые задачи, поскольку соответствующие модели достаточно сложны. Такие задачи могут быть статическими и динамическими. Из статичес­ких задач наиболее простыми представляются моделирование распределения поля температур или электростатического поля. И динамических задач, модели которых рассматривались в школьном курсе информатики, известна задача теплопроводности в стержне — вероятно, самая простая задача такого рода.

Основные цели, преследуемые в данном разделе, таковы:

• углубление математического и физического образования учащихся;

• выработка навыков визуализации абстракций — важной задачи для прикладной информатики в целом.

Остановимся на методике решения задачи моделирования распределения статических полей. Универсальным способом визуализации физического поля, распределенного в некоторой плоскойобласти или в некотором объеме, является построение его изолиний (изоповерхностей).

Как показывает опыт, на данном этапе в подавляющем большинстве случаев следует ограничиться моделированием распределений полей в плоскости. Объемные построения требуют большого времени и непосильны многим учащимся.

Приступая к рассказу о построении изолиний, вначале приводим доводы в пользу того, что этот прием является удобным для визуализации поля. В курсе физики учащиеся, скорее всего, видели картины силовых линий электрического поля. Построение силовых линий, однако, задача более сложная, чем построение линий равного потенциала (изолиний), а информации дает не больше. Продемонстрируйте учащимся картины изолиний поля, создава­емого изолированным зарядом, парой равных зарядов и покажите, как по ним отчетливо видна общая картина поля. Другими примерами могут быть изотермы, которыми иногда сопровожда­ют прогноз погоды, линии тока жидкости, изолинии концентра­ции вредных примесей в окружающей среде и т.д.

Далее переходим к технике построения изолиний. За основу можно взять процедуру, описанную в пособиях [5, 9].

Задачи, уместные для отладки первых навыков такого модели­рования, очень просты. Пробной (тестовой) задачей является мо­делирование поля одиночного заряда, для которого ответ очеви­ден: любая изолиния — окружность. Затем следуют простые сим­метричные комбинации зарядов.

Обсудите теперь методику проведения занятий по моделирова­нию процесса переноса тепла в стержне. Эта тема уместна лишь при достаточно высокой математической подготовке учащихся, потому что в данном разговоре трудно избежать появления диф­ференциальных уравнений (хотя и возможно), причем уравнений в частных производных. Однако опыт показывает, что если не обсуждать сложных вопросов о таких уравнениях, не вдаваться в общие математические рассуждения, то на эмпирическом уровне тема вполне посильна для хорошо подготовленных учащихся и воспринимается ими с интересом.

Последовательность построения учебного процесса может быть следующей. О том, что такое теплопроводность, интуитивно все знают. Если рассматривать простейшую ситуацию — распространение тепла в однородном стержне с теплоизолированной боковой поверхностью — то понятно, что температура (основная характеристика процесса) является функцией единственной координаты и времени. В простейшей модели боковая поверхность стержня считается теплоизолированной, т. е. через нее нет обмена теплом с окружающей средой.

Вывод у равнения теплопроводности можно найти в ряде пособий, причем надо идти не от общего к частному (такой путь школьникам непосилен), а обращаться именно к простейшей ситуации однородного стержня с теплоизолированной боковой поверхностью. При этом, как обычно в таких случаях, вначале появляются приближенные конечно-разностные уравнения, затем от них (с помощью двух предельных переходов — по координате и по времени) переходят к дифференциальным уравнениям. Поскольку при компьютерном моделировании мы всецело опираемся на численные методы, то для решения дифференциальных уравнений мы вновь строим конечно-разностную модель. Такая «двухъярусная» дискретизация весьма поучительна с точки зрения информатики. Естественно, нескольких пунктов этой программы можно избежать и вообще исключить появление дифференциальных уравнений, хотя кое-что при этом остается недоговоренным; у математика такой подход порождает чувство неудовлетворенности.

Уравнение теплопроводности сопровождается начальными и краевыми условиями, делающими постановку задачи физически однозначной. (Последнее утверждение доказать на данном уровне изложения невозможно, но интуитивно приемлемые доводы привести легко.) Начальное условие задает распределение температуры в стержне в начальный момент времени; краевые условия (их должно быть в данном случае два) указывают в простейшей варианте (которым вполне достаточно в данном случае ограничиться), какая температура поддерживается на концах стержня.

Подчеркнем, что моделирование процесса теплопроводности связано с дискретизацией как временного изменения температуры, так и пространственного. Если для пространственных производных использовать простейшие центрально-разностные аппроксимации, а по времени — схему Эйлера, то величины {и_i^к} — значения температуры в i-ом узле пространственной сетки в k-ймомент времени — приближенно находятся из системы весьма простых формул.

Если задаться целью получения уравнений модели сразу в конечно-разностной форме (минуя дифференциальную), то возникает нетривиальная задача вывода соответствующих формул, решение которой можно позаимствовать в задачнике [6].

При описанном моделировании не следует забывать о возможной неустойчивости простейшей разностной схемы. Прежде всего, следует объяснить учащимся само понятие «неустойчивость». Рассуждаем примерно следующим образом. Расчетные формулы появились как дискретная аппроксимация непрерывного процесса. Чем мы расплачиваемся за дискретизацию? Первая «расплата» очевидна: мы получаем приближенное описание процесса. Числа {и_i^к} отнюдь не являются точными значениями температуры. Для увеличения точности результатов кажется естественным уменьшать шаги по координате и по времени, но здесь мы сталкиваемся со второй проблемой. Ее природа достаточно сложна, она уходит как в аппроксимацию производных конечными разностями, так в накопление погрешностей округлений. При неудачном выборе шагов по координате и по времени решение начинает «раскачиваться» и перестает походить на истинное. В данном случае достаточно ограничиться приведением критерия устойчивости метода, приводящего к используемым расчетным формулам.

Тема «Имитационные стохастические модели»

Имитационное моделирование может стать существенной час­тью профильного курса информатики, ориентированного на мо­делирование. Включение метода имитационного компьютерного моделирования в профильный курс, ориентированный на моде­лирование, работа учащихся с имитационными моделями сред­ней сложности представляют несомненный интерес и пользу, по­скольку расширяют и обобщают представление о методе модели­рования и его возможностях.

Идея имитационного моделирования интуитивно ясна и при­влекательна. В основе этого метода — теория вычислительных си­стем, статистика, теория вероятностей.

Начало изучения темы — лекция об имитационном моделиро­вании случайных процессов. К сожалению, в российской школе понятия теории вероятностей и математической статистики лишь начинают внедряться в курс математики, и учителю следует быть готовым к тому, чтобы самому сделать введение в этот важней­ший для формирования мировоззрения и математической культу­ры материал. Приведем план соответствующей вводной лекции.

1. «Случайность» как фундаментальное математическое понятие. Случайные события и их вероятности.

2. Дискретные и непрерывные случайные величины. Дифференциальная функция распределения непрерывной случайной величины (плотность вероятности).

3.Примеры типичных функций распределения. Равновероятное Определение. Нормальное распределение и представление об его особой значимости в связи с центральной предельной теоремой теории вероятностей.

4.Метод статистических испытаний в моделировании случайных процессов. Представление о статистической обработке результатов, получаемых при использовании метода статистических испытаний. Понятия «доверительный интервал», «доверительная вероятность». Вычисление средних значений испытуемых величин и оценка их достоверности.

5.Описание принципов имитационного моделирования. Отметим ключевые моменты, которые следует донести до учащихся. Имитацию целесообразно использовать:

• если она позволяет экспериментально исследовать сложные внутренние взаимодействия в рассматриваемой системе;

• при изучении воздействия на функционирование системы некоторых информационных и организационных изменений, а также изменений во внешней обстановке; для этого в модель системы вносят изменения и наблюдают влияние этих изменений на изменение системы;

• при детальном наблюдении имитируемой системы, что позволяет лучше понять систему и разработать такие предложения по ее имитации, которые были бы невозможны без имитации;

• если имитация сложных систем может дать представление о том, какие из переменных системы наиболее существенны и как эти переменные взаимодействуют.

Подчеркнем, что речь идет об элементарном введении в круг обсуждаемых понятий. В принципе сделать это можно не более, чем за два-три урока.

После этого обсуждаем технические вопросы, связанные с ге­нерацией на ЭВМ последовательностей случайных чисел с задан­ным законом распределения. Опираться при этом можно на про­стой факт: в каждом языке программирования есть датчик равно­мерно распределенных случайных чисел на отрезке от 0 до 1. На данном этапе нецелесообразно вдаваться в сложный вопрос о принципах его реализации. Опираясь на эти датчики, показыва­ем, как можно устроить:

а) генератор равномерно распределенных случайных чисел на любом отрезке [а, Ь];

б) генератор случайных чисел под практически любой закон распределения (например, используя интуитивно ясный метод «отбора — отказа»).

Одним из вариантов отработки навыков имитационного стоха­стического моделирования является рассмотрение задачи моделирования очереди в системе массового обслуживания. Указанные системы элементарны для понимания постановки задач, имеют широкое прикладное значение.

Начать рассмотрение этой задачи целесообразно с обсуждения истории решения проблем массового обслуживания (задача Эрланга об обслуживании запросов на телефонной станции). Затем следует обзор типичных задач этой науки. Следует сказать о постановке задач в аналитической форме и о трудностях их решений о том, что имитационное компьютерное моделирование при решении задач массового обслуживания, реализуемое в виде метода статистических испытаний (метода Монте-Карло), хоть и не является в теории массового обслуживания основным, но играет в ней важную роль. Основная линия в ней — получение аналитических результатов, т. е. представленных формулами. Однако возможности аналитических методов весьма ограничены, в то время как метод статистических испытаний универсален и весьма прост для понимания (по крайней мере, кажется таковым).

Затем следует рассмотреть простейшую задачу, которую можно формулировать на примере формирования и обслуживания очереди в магазине с одним продавцом. В этот магазин случайным образом входят покупатели. Если продавец свободен, то он начинает обслуживать покупателя сразу, иначе покупатель становится в очередь. Детали постановки и решения этой задачи методом статистического моделирования можно найти в книгах [9, 33]. Отметим, что на первом этапе моделирования распределения случай­ных величин на входе можно принять равновероятными, что хоть и не реалистично, но снимает ряд трудностей (для генерации слу­чайных чисел можно просто использовать встроенный в язык про­граммирования датчик).

Обратите внимание учащихся на то, какие вопросы ставятся в первую очередь при моделировании систем такого вида? Во-пер­вых, это вычисление средних значений (математических ожида­ний) некоторых случайных величин. Например, какое среднее время приходится стоять в очереди к прилавку? Или найти сред­нее время, проведенное продавцом в ожидании покупателя.

Задача учителя, в частности, состоит в том, чтобы разъяснить, что выборочные средние величины сами по себе — случайные величины; в другой выборке того же объема они будут иметь дру­гие значения (при больших объемах выборки — не слишком отли­чающиеся друг от друга). Далее возможны варианты, например, в более подготовленной аудитории можно показать способ оцени­вания доверительных интервалов, в которых находятся матема­тические ожидания соответствующих случайных величин при за­данных доверительных вероятностях (известных из математической статистики методами без попытки обоснования). В менее подготов­ленной аудитории можно ограничиться чисто эмпирическим утверждением, к примеру, если в нескольких выборках равного объема средние значения совпали в некотором десятичном знаке, то этот знак, скорее всего, верен. Если при моделировании не удается достичь желаемой точности, следует увеличить объем выборки.

В наиболее подготовленной в математическом отношении аудитории можно ставить вопрос: каково распределение случайных величин, являющихся результатами статистического моделирования, при заданных распределениях случайных величин, являются его входными параметрами? Поскольку изложение соответствующей математической теории в данном случае невозможно, следует ограничиться эмпирическими приемами: построением гистограмм итоговых распределений и сравнением их с несколькими типичными функциями распределения.

После отработки первичных навыков указанного моделирования переходим к более реалистической модели, в которой входные потоки случайных событий распределены по Пуассону. Это потребует от учащихся дополнительно освоить метод генерирования последовательностей случайных чисел с указанным законом распределения.

В рассмотренной задаче, как и в любой более сложной задаче об очередях, может возникнуть критическая ситуация, когда очередь неограниченно растет со временем. В самом деле, если люди заходят в магазин очень часто (или продавец работает слишком медленно), то очередь начинает нарастать, и в любой системе конечным временем обслуживания наступит кризис. Моделирование приближения к критической ситуации по мере возрастания одного из параметров — интересная исследовательская задача.

На примере задачи об очереди отрабатываются сразу несколь­ко новых понятий и навыков, таких как:

• понятие о случайных процессах;

• понятие и простейшие навыки имитационного моделирования;

• построение оптимизационных имитационных моделей;

• построение многокритериальных моделей (путем решения задач о наиболее рациональном обслуживании покупателей в сочетании с интересами владельца магазина).

Тема «Моделирование динамики развития популяций»

В данной теме ограничимся обсуждением методики проведения занятий по моделированию некоторых процессов, составляющих основу классической экологии (т. е. процессов развития отдельных популяций и их взаимодействия). В такой постановке этот материал может быть полезен для проведения нескольких уроков в пределах предмета, в котором моделирование экологических процессов является не основой, а частью. Такой выбор обусловлен следующими причинами. Во-первых, соответствующие модели достаточно просты и изучены, постановка их вполне очевидна и в познавательном плане интересна и полезна. Во-вторых, модели распространения загрязнений окружающей среды, которые успешно применяют в современной социальной экологии, требуют использования весьма сложного математического аппарата, да и сами еще не вполне устоялись.

С другой стороны, возможны профильно-ориентированные на экологию курсы информатики. Для таких курсов рассматриваемого в данном параграфе материала недостаточно. Дополнительный материал на эту тему можно найти, к примеру, в пособиях.

Вводная беседа в этой теме может быть посвящена введению в проблематику классической экологии и использование в нейтематических моделей. Следует дать определения таким понятиям, как «популяция», «сообщество», «внутривидовая конкурен­та» «межвидовая конкуренция».

Математические модели в экологии используются практически с момента возникновения этой науки. И хотя поведение организмов в живой природе гораздо труднее адекватно описать средствами математики, чем самые сложные физические процессы, модели помогают установить некоторые закономерности и общие тенденции развития отдельных популяций, а также сообществ. Кажется удивительным, что люди, занимающиеся живой природой воссоздают ее в искусственной математической форме, но есть веские причины, которые стимулируют эти занятия. Вот ос­новные цели создания математических моделей в классической экологии:

1. Модели помогают выделить суть или объединить и выразить с помощью нескольких параметров важные разрозненные свойства большого числа уникальных наблюдений, что облегчает экологу анализ рассматриваемого процесса или проблемы.

2. Модели выступают в качестве «общего языка», с помощью которого может быть описано каждое уникальное явление, и относительные свойства таких явлений становятся более понятными.

3. Модель может служить образцом «идеального объекта» или идеализированного поведения, при сравнении с которым можно оценивать и измерять реальные объекты и процессы.

Модель считается адекватной рассматриваемому явлению толь­ко в том случае, если она выполняет одну из указанных выше фун­кций.

При проведении беседы следует обратить внимание учащихся на то, что привлечение компьютеров существенно раздвинуло границы моделирования экологических процессов. С одной сторо­ны, появилась возможность всесторонней реализации сложных математических моделей, не допускающих аналитического иссле­дования, с другой — возникли принципиально новые направления, и, прежде всего — имитационное моделирование. После вводной лекции приступаем к построению и исследованию конкретных моделей. Методически уместно начать это с рассмотрения развития популяций с дискретным размножением, после чего следует плавный переход на популяции с непрерывным размножением. Естественная последовательность рассмотрения такова:

Ø динамическое моделирование численности изолированной популяции с дискретным размножением:

a. при отсутствии внутривидовой конкуренции;

b. при наличии внутривидовой конкуренции;

Ø динамическое моделирование численности изолированной популяции с непрерывным размножением:

a. при отсутствии внутривидовой конкуренции;

b. при наличии внутривидовой конкуренции;

Ø динамическое моделирование взаимодействия популяции.

а) состоящих в отношениях межвидовой конкуренции;

б) состоящих в отношениях «хищник— жертва»;

Ø имитационное моделирование развития популяции и взаимодействия популяций.

Примеры ряда моделей, обозначенных выше, можно найти в пособиях [5, 9, 22, 27, 30, 35]. Обсудим методику их построения и исследования на нескольких примерах.

Пример. Моделирование развития изолированной популяции с дискретным размножением с учетом внутривидовой конкуренции.

Рассматриваются биологические виды, для которых потомки и предки не сосуществуют во времени (многочисленные растения насекомые и др.). Тогда последовательные значения численности популяции можно представить последовательностью N_o, N₁... Если нет никаких причин ограничения численности популяции, тогда возникает простейшая очевидная модель: N_t+1 = R *N_t, где R — коэффициент воспроизводства. Решение этой модели очевидно: N_t= N₀- R^t, и при R >1 численность популяции нарастает по геометрической прогрессии.

Даже эта простейшая модель заслуживает обсуждения. Она вы­ражает то, что в литературе иногда называют «законом Мальтуса». Очевидно, что долго неограниченно возрастать популяция не может. Простейший способ учета внутривидовой конкуренции свя­зан с гипотезой о том, что коэффициент воспроизводства не есть константа, а зависит от численности популяции, спадая по мере ее роста. На этом этапе следуют разъяснить учащимся методику построения моделей в сфере знаний, где основным способом ис­следования являются наблюдения, в которой точные математи­ческие законы отсутствуют в силу сложности системы (в отличи от, например, физики). В такой ситуации делаются достаточно про­извольные допущения, в значительной мере оправдываемые простотой, а полезность модели определяется путем сопоставления ее решений с закономерностями поведения реальных систем.

Проиллюстрируем это простым соображением. Итак, надо учесть, что величина R монотонно спадает с ростом величины N. Реального вида этого спада мы не знаем; его можно представить множеством способов с использованием общеизвестных элементарных функций, а если надо, то и выходом из этого класса. Модель, в основу которой положена простейшая из таких функций, выглядит следующим образом:

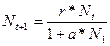
Методика исследования этой модели и ряда других описана в указанных выше пособиях. Полезность модели следует их того, что описываемое ею поведение численности популяций многократно наблюдалось экологами в природе.

После этого ставим вопрос: достаточно ли этой модели для качественного описания развития любой популяции с дискретным размножением? Ответ может последовать лишь из того, наблюдались ли качественно иные динамики развития таких популяций, и является положительным. В природе наблюдались существенно более сложные процессы, нежели монотонное возрастание численности популяций с выходом на стационар, предсказываемое описанной выше моделью. Поэтому продолжился поиск более адекватных моделей.

В частности, целесообразно рассмотреть модель, предсказыва­ющую четыре качественно разных типа динамики численности популяций (в зависимости от соотношения значений параметров): монотонное возрастание с выходом на стационар, колебательное установление стационарной численности, регулярное колебатель­ное изменение (так называемые предельные циклы) и хаотичес­кое поведение без каких-либо видимых закономерностей. Все эти типы динамик наблюдаются в природе.

Методика изучения сложных движений зависит от математи­ческой подготовки учащихся. Чаще всего предельные циклы и ха­отическое поведение приводим описательно, иллюстративно, не стремясь дать определение этим сложным процессам. В классах же с высоким уровнем математической подготовки и выраженным интересом учащихся обсуждение этих вопросов может быть суще­ственным элементом развития математических интересов.

При изучении более сложных моделей, выраженных диффе­ренциальными уравнениями, методика исследования в основном остается та же. Она включает следующие этапы:

• постановку проблемы, введение терминологии, описание поведения соответствующих природных систем;

• построение математической модели;

• попытку качественного исследования модели, включая построение диаграмм на фазовой плоскости параметров модели;

• численное решение дифференциальных уравнений (как правило, простейшими из методов либо путем использования готовых программ).

Совсем иной является методика построения имитационных моделей экологических процессов. Ограничимся формулировкой одной из задач [5], на которой можно отработать построение такой модели.

Пример. Разработать имитационную модель системы «хищник-жертва» По следующей схеме.

«Остров» размером 20x20 заселен дикими кроликами, волками и волчицами. Имеется по несколько представителей каждого вида. Кролики в каждый момент времени с одинаковой вероятностью 1/9 передвигаются в один из восьми соседних квадрата (за исключением участков, ограниченных береговой линией) или просто сидят неподвижно. Каждый кролик с вероятностью 0,2 превращается в двух кроликов. Каждая волчица передвигается случайным образом, пока в одном из соседних восьми квадратов окажется кролик, за которым она охотится. Если волчица и кролик оказываются в одном квадрате, волчица съедает кролика получает одно очко. В противном случае она теряет 0,1 очка.

Волки и волчицы с нулевым количеством очков умирают. В начальный момент времени все волки и волчицы имеют 1 очко.

Волк ведет себя подобно волчице до тех пор, пока в соседних квадратах не исчезнут все кролики; тогда если волчица находится в одном из восьми близлежащих квадратов, волк гонится за ней.

Если волк и волчица окажутся в одном квадрате и там нет кро­лика, которого нужно съесть, они производят потомство случайного пола.

Пронаблюдайте за изменением популяции в течение некоторого периода времени. Проследите, как сказываются на эволюции популяций изменения параметров модели.