Показательное распределение

Рис. 10.10

Определим числовые характеристики равномерного распределения.

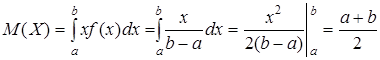. (10.19)

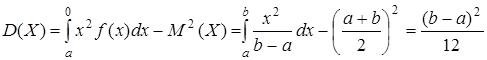; (10.20)

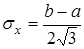. (10.21)

Очевидно, что моды нет, а медиана равна математическому ожиданию.

Вероятность попадания в интервал (α, β) равномерно распределенной случайной величины задается следующей, легко выводимой формулой:

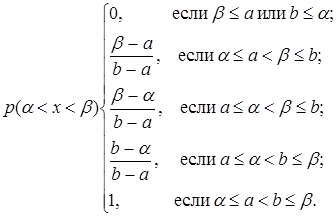(10.22)

Равномерным распределением можно аппроксимировать ошибки измерений, когда измеренное значение округляют до ближайшего целого на шкале измерительного прибора.

Найдем закон распределения линейной функции Y равномерно распределенной случайной величины Х, Y = (cX + d), где с, d – данные числа.

Если 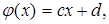то 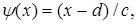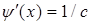. Когда значения случайной величины Х принадлежат интервалу (a, b), значения случайной величины Y принадлежат интервалу (ca + d; cb +d); следовательно,

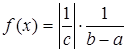, если 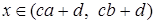; в противном случае .

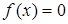Вновь получено равномерное распределение – на этот раз на интервале (ca + d, cb + d). (Если c < 0, то левая граница интервала – число cb +d, правая - число ca + d). ]

Случайная величина Х имеет показательное распределение, если ее плотность вероятности задается формулой

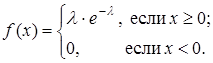(10.23)

Параметр закона λ должен быть больше нуля.

Опишем функцию распределения F (x) показательного закона. Если х £ 0, то, очевидно, F (x) = 0. Пусть х > 0. Тогда

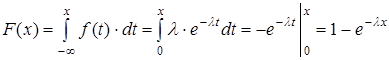, таким образом

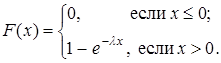(10.24)

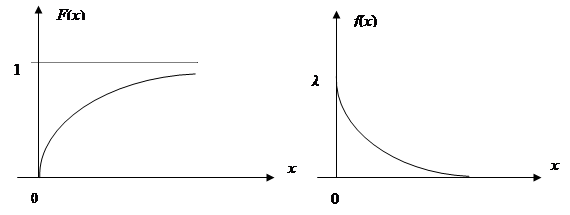
Графики функций F (x) и f (x) показаны на рис. 10.11.