2014-02-12
621
Рис. 10.11
Найдем числовые характеристики показательного распределения.
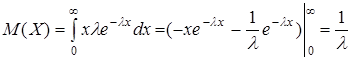. (10.25)
.
; 
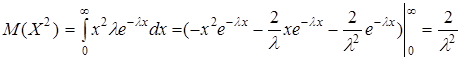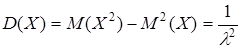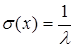. (10.26)
Ясно, что мода равна нулю. Найдем медиану. Из условия
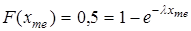следует, что 
.
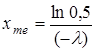Вероятность попадания в интервал (α, β),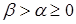 
, равна
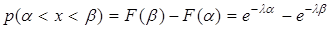. (10.27)
Показательное распределение используется, например, в теории массового обслуживания.
Случайная величина Х распределена по нормальному закону (закону Гаусса), если ее плотность вероятности задается формулой
, 
,
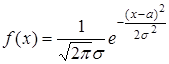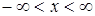где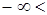 
а < ¥ и σ > 0 – параметры закона.
График функции плотности вероятности нормального закона показан на рис. 10.12.
 |
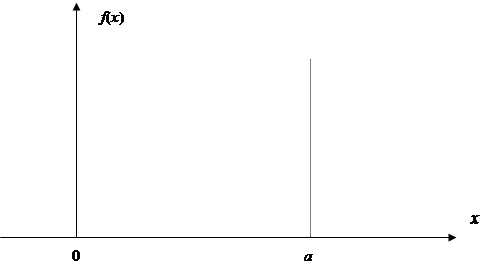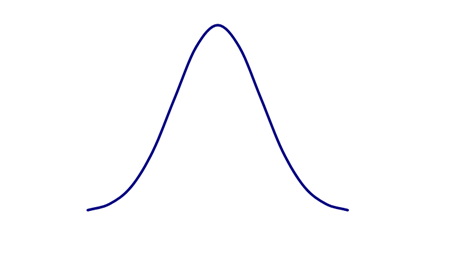Рис. 10.12
График симметричен относительно прямой х = а.
Ниже показательная функция ех будет иногда обозначаться EXP (х) для удобства чтения текста.
Найдем числовые характеристики нормального закона. Ясно, что мода и медиана вследствие наличия оси симметрии равны а.
.
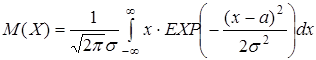Положим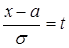 
, тогда 
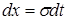, откуда
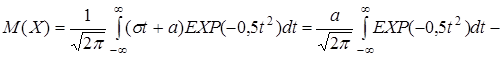
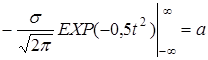, так как 
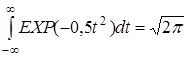- это известный из курса анализа интеграл Пуассона.
Математическое ожидание нормального закона равно значению параметра а.
|
|
|
,
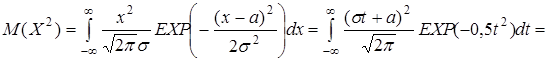
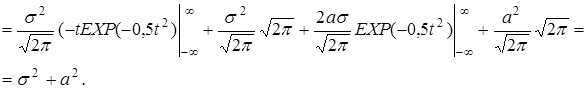Итак, D (X) = σ 2, σ (X) = σ. Среднее квадратическое отклонение нормально распределенной случайной величины равно значению параметра σ.
Вычислим вероятность того, что нормально распределенная случайная величина Х примет значение из интервала (α, β).
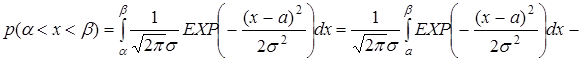
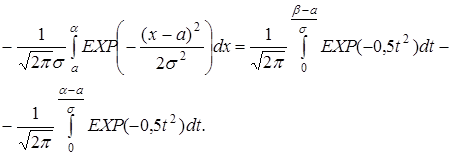
Функция
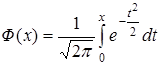(10.28)
называется функцией Лапласа. Для нее составлены таблицы, по которым, зная аргумент х, можно найти величину Φ (х). Можно, конечно, решить обратную задачу: по значению функции Лапласа найти значение аргумента.
Укажем три простых свойства функции Лапласа:
1. 
.
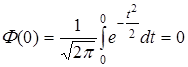2. 
.
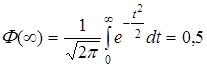На самом деле уже для значений аргумента х ³ 5 можно считать, что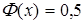 
.
3. 
.
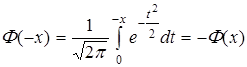Таким образом, функция Лапласа нечетна.
Мы показали, что
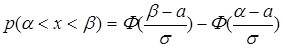. (10.29)
Теперь легко описать функцию распределения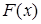 
нормального закона с параметрами a и s. В самом деле
.
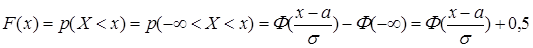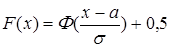(10.30)
В некоторых пособиях по теории вероятностей приводятся таблицы функции
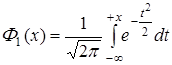. Нетрудно видеть, что 
,
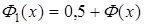так что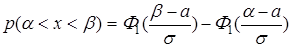 
.
Иногда приводится таблица значений функции
, 
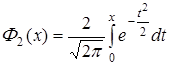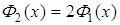, поэтому
.
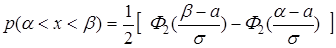Для интервала |Х - а| < δ имеем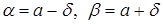 
, поэтому
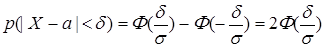. (10.31)
Опишем еще закон распределения линейной функции Y = cX + d нормально распределенной случайной величины Х, где c и d - заданные числа. Случайная величина Y принимает значения на всей числовой оси.
.
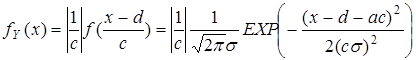Получена функция плотности нормального закона с параметрами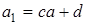 
, 
.
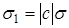Линейная функция нормально распределенного аргумента также нормально распределена.
Нормальное распределение довольно часто встречается при решении практических задач. В приложении приведена таблица нормального распределения (таблица функции Лапласа).
