Построение опорных планов, а также преобразование их будем производить непосредственно в распределительной таблице. Если в плане перевозок переменная хik равна некоторому числу а ≠ 0, то это число записываем в соответствующую клетку (i; k) и считаем ее занятой или базисной, если же хik = 0, то клетку (i; k) оставляем свободной. При этом число занятых опорным планом клеток в соответствии с теоремой 5.2 должно быть равно т+п -1, а остальные тп - (т+п- 1) = (т -1) (п- 1) клеток будут свободными.
Рассмотрим правило «северо-западного угла». Сущность его состоит в следующем. Пользуясь табл. 5.1, будем распределять груз, начиная с загрузки левой верхней, условно называемой северо-западной, клетки (1; 1), двигаясь затем от нее по строке вправо или по столбцу вниз. В клетку (1; 1) занесем меньшее из чисел a 1, b 1, т. е. x 11 = min (a 1, b 1). Если a 1> b 1, т. е. x 11 = b 1 и первый потребитель В 1 будет полностью удовлетворен. В дальнейшем 1-й столбец таблицы в расчет не принимается; в нем переменные хik =0 для i =2, т.
Двигаясь вправо по первой строке таблицы, заносим в соседнюю клетку (1; 2) меньшее из чисел a 1- b 1, и b 2, т. е. x 12 = min (a 1- b 1, b 2). Если a 1- b 1< b 2, то запасы первого поставщика исчерпаны и первая строка таблицы в дальнейшем в расчет не принимается. Переходим к аналогичному распределению запаса груза второго поставщика.
Если a 1< b 1, т. е. x 11 = a 1. При этом запас первого поставщика будет исчерпан, а потому хik =0 для k =2, п. Первая строка из дальнейшего рассмотрения исключается. Переходим к распределению запасов второго поставщика. В клетку (2; 1) заносим наименьшее из чисел (а 2, b 1- а 1).
Заполнив таким образом клетку (1; 2) или (2; 1), переходим к загрузке следующей клетки по второй строке либо по второму столбцу. Процесс распределения по второй, третьей и последующим строкам (столбцам) производится аналогично распределению по первой строке или первому столбцу до тех пор, пока не исчерпаются ресурсы. Последней заполняется клетка (т; п).
Проиллюстрируем правило «северо-западного угла» на примере.
Пример 5.1. Составить план перевозок зерна из районов А1, А2, А3 и А4, в которых запасы составляют соответственно 800, 700, 1000 и 500 тыс.ц, на три элеватора В1, В2 и В3 мощностью 1000, 1100 и 900 тыс.ц. Затраты на перевозку 1 ц зерна из районов на элеваторы приведены в табл. 5.2.
Таблица 5.2
| Районы | Элеваторы | Запас в районе | ||
| В1 | В2 | В3 | ||
| Затраты на перевозку 1 ц, руб. | ||||
| А1 | ||||
| А2 | ||||
| А3 | ||||
| А4 | ||||
| Мощность элеватора |
Решение. Установим характер задачи. Поскольку
800+700+1000+500=1000 + 1100+900=3000,
заключаем, что данная ТЗ обладает закрытой моделью. В клетку (1; 1) табл. 5.3 помещаем x 11 = min (800, 1000) =800 тыс. ц зерна. Весь запас зерна района А1 отгружен на элеватор В1. Недостающее количество зерна на элеватор В1 поставляется из района А2: в клетку (2; 1) помещаем x 21 = min (700, 1000 - 800) =200 тыс. ц. В этом случае мощность элеватора В1 будет полностью использована. Остаток зерна района А2 отправляем на элеватор В2: в клетку (2; 2) помещаем x 22 = min (700 - 200, 1100) =500 тыс. ц зерна. Запас зерна района А2 исчерпан, и переходим к перевозке зерна района А3. В клетку (3; 2) помещаем x 32 = min (1000, 1100 - 500) = 600 тыс. ц зерна. Мощность элеватора В2 полностью использована. Поставку зерна производим на элеватор В3. В клетку (3; 3) помещаем x 33 = min (900, 1000 - 600) =400 тыс. ц зерна. Отгрузка зерна из района А3 полностью произведена. Производим отгрузку зерна из района А4. В клетку (4; 3) помещаем x 43 = min (500, 900 - 400) =500 тыс. ц зерна. В результате полной отгрузки зерна на элеваторы получили план перевозок X 1 (табл. 5.3).
Таблица 5.3
| Районы | Элеваторы | Запас в районе | ||
| В1 | В2 | В3 | ||
| Затраты на перевозку 1 ц, руб. | ||||
| А1 | ||||
| А2 | ||||
| А3 | ||||
| А4 | ||||
| Мощность элеватора |
Суммарные расходы на перевозку зерна составят:
f (X 1) = 3*800+7*200+2*500+3*600+3*400+7*500=12 100 руб.
Рассмотрим правило «минимального элемента». Сущность его состоит в следующем. Просматриваются тарифы табл. 5.1 и в первую очередь заполняется клетка с минимальным значением тарифа. При этом в клетку записывается максимально возможное значение поставки. Затем из рассмотрения исключают строку, соответствующую поставщику, запасы которого полностью израсходованы, или столбец, соответствующий потребителю, спрос которого полностью удовлетворен. После этого из оставшихся клеток таблицы снова выбирают клетку с наименьшим тарифом. Процесс распределения заканчивается, когда все запасы поставщиков исчерпаны, а спрос потребителей полностью удовлетворен. В результате получаем опорный план, который должен содержать т+п- 1 загруженных клеток. В процессе заполнения таблицы могут быть одновременно исключены строка и столбец. Так бывает, когда полностью исчерпывается запас груза и полностью удовлетворяется спрос (вырожденная задача). В этом случае в свободные клетки надо записать число 0 - «нуль-загрузка», условно считая такую клетку занятой. Однако число 0 записывается в те свободные клетки, которые не образуют циклов с ранее занятыми клетками.
Пример 5.2. Проиллюстрируем правило «минимального элемента» для транспортной задачи, представленной табл. 5.2, и сравним значения целевых функций для планов, полученных по правилу «северо-западного угла» и правилу «минимального элемента».
Решение. Просматривая табл. 5.2, замечаем, что минимальные затраты на перевозку зерна соответствуют маршруту А2-В2, поэтому в клетку (2; 2) табл. 5.4 помещаем x 22 = min (700, 1100) =700 тыс. ц зерна. В этом случае вторая строка таблицы в дальнейшем в расчет не принимается, так как запас зерна в районе А2 полностью доставлен на элеватор В2.
Просматриваем оставшиеся клетки таблицы. Наименьшие тарифы имеют клетки (1; 1), (3; 2) – 4. В клетку (1; 1) помещаем x 11 = min (800, 1000) = 800 тыс. ц, а в клетку (3; 2) x 32 = min (1000, 1100 - 700) =400 тыс. ц.
Далее по величине тарифа следует загружать клетки (3; 1), (4; 2),
(2; 3). Однако в результате загрузки клеток (1; 1), (2; 2), (3; 2) запас зерна в районах А1 и А2 и частично в районе А4 исчерпан. Мощность элеватора В2 полностью использована, а мощность элеватора В1 использована на
800 тыс. ц. Поэтому помещаем необходимое количество зерна в клетку (3; 1): x 31 = min (1000 - 400, 1000 - 800) = 200 тыс. ц. После этого мощность элеватора В1 полностью использована. Остался элеватор В3, который может принять зерно из районов А3 и А4. В районе А3 осталось зерна
1000 – 400 - 200=400 тыс. ц,
а в районе А4 - 500 тыс. ц. В клетки (3; 3); (4; 3) помещаем необходимые количества зерна: x 33=400 тыс. ц, x 34=500 тыс. ц.
Таблица 5.4
| Районы | Элеваторы | Запас в районе | ||
| В1 | В2 | В3 | ||
| Затраты на перевозку 1 ц, руб. | ||||
| А1 | ||||
| А2 | ||||
| А3 | ||||
| А4 | ||||
| Мощность элеватора |
В результате полного распределения зерна получаем план Х 2, для которого значение целевой функции
f (X 2) = 3*800+2*700+4*200+3*400+3*400+7*500 =11 300 руб.
Сравнивая значения целевых функций для планов Х 1 и Х 2, полученных по правилам «северо-западного угла» и «минимального элемента», замечаем, что транспортные расходы по плану Х 2 на перевозку зерна из районов на элеваторы меньше на 800 руб.
Будет ли этот план оптимальным? Чтобы ответить на этот вопрос, необходимо знать признак оптимальности.
Теорема 5.3. Если план 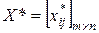 транспортной задачи является оптимальным, то ему соответствует система из m+n чисел
транспортной задачи является оптимальным, то ему соответствует система из m+n чисел 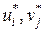 , удовлетворяющих условиям
, удовлетворяющих условиям 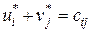 для
для 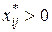 и
и 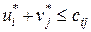 для
для 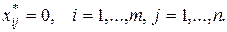
Числа 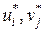 называются потенциалами соответственно i -го поставщика и j -го потребителя.
называются потенциалами соответственно i -го поставщика и j -го потребителя.
Доказательство. Транспортную задачу можно рассматривать как двойственную задачу к некоторой исходной задаче, решаемой на максимум. Построим эту задачу. Так, если i -му ограничению двойственной задачи 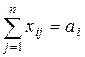 в исходной задаче соответствует переменная
в исходной задаче соответствует переменная 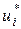 , а j -му ограничению
, а j -му ограничению 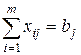 – переменная
– переменная 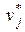 , то исходной будет задача: найти максимальное значение функции
, то исходной будет задача: найти максимальное значение функции
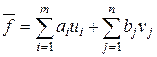
при ограничениях
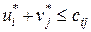 ,
,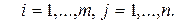
Оптимальным для двойственной задачи является план х*,а для исходной Y* = (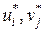 ). Для пары взаимодвойственных задач на основании первой теоремы двойственности имеет место равенство
). Для пары взаимодвойственных задач на основании первой теоремы двойственности имеет место равенство 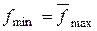 , а по второй теореме двойственности выполняются условия
, а по второй теореме двойственности выполняются условия 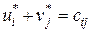 для
для 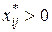 и
и 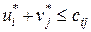 для
для 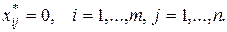
Из теоремы следует, что для оптимального плана ТЗ необходимо выполнение условий:
1) каждой занятой клетке в распределительной таблице соответствует сумма потенциалов, равная тарифу этой клетки, т. е. 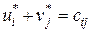 ;
;
2) каждой свободной клетке соответствует сумма потенциалов, не превышающая тарифа этой клетки, т. е. 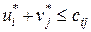
Доказанная теорема носит название теоремы о потенциалах. На ней основан специальный метод решения ТЗ, названный методом потенциалов.
 2014-02-12
2014-02-12 1187
1187








