Чистые стратегии матричной игры

Различают стратегии чистые и смешанные. Чистая стратегия A_i (i =1,…, m) первого игрока (чистая стратегия B_j (j =1,…, п) второго игрока) - это возможный ход первого (второго) игрока, выбранный им с вероятностью, равной 1.

Теорема 6.1. В матричной игре нижняя чистая цена игры не превосходит верхней чистой цены игры, т. е. .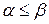

Доказательство. Положим:

.

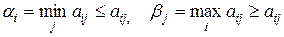Объединив эти соот­ношения, получим

.

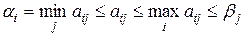Отсюда 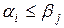. Это неравенство справедливо для любых i и j, следовательно,

,

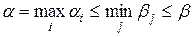что и требовалось доказать.

Если для чистых стратегий А_i, В_j игроков А и В соот­ветственно имеет место равенство 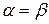, то пару чистых стратегий (А_i, В_j) называют седловой точкой матричной игры, элемент a_ij матрицы, стоящий на пересечении i -й строки и j -го столбца – седловым элементом платежной матрицы, а число 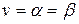- чистой ценой игры.

Наличие седловой точки означает наличие чистых стратегий игроков, гарантирующих каждому из них результат не хуже одной и той же определенной величины.

Из сказанного выше ясно, как проверять платежную матрицу на наличие седловой точки:

– в каждой строке находится минимальный элемент, а среди них берется максимальный;

– в каждом столбце находится максимальный, а среди них берется минимальный;

– если эти два элемента совпадают, то матрица имеет седловую точку, в противном случае нет.

Седловая точка может быть не единственной. Для пояснения рассмотрим пример.

Пример 6.3. Найти седловые точки следующих платежных матриц:

1)		В1	В2	В3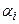
	А1
	А2
	А3

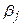
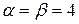
Седловая точка , .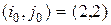

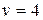2)		В1	В2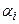
	А1		-2	-2
	А2	-2		-2

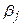
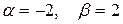
Седловой точки нет ().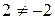

3)		В1	В2	В3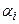
	А1
	А2

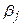
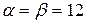
Две седловые точки (1, 1), (1, 3), цена игры 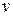= 12.

Поскольку и справа, и внизу в финал для сравнения выходят по одному числу, постольку получается, что цена игры для разных седловых точек (если их несколько) одна и та же.

При наличии у платежной матрицы седловой точки, естественно, выбирают стратегии, соответствующие этой точке. Такое решение гарантирует одному из игроков «выигрыш» не меньше определенной величины (цены игры 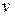), другому – «проигрыш» не больше этой величины. Отклонение от этих стратегий может дать одному из игроков выигрыш как больше, так и меньше цены игры (никаких гарантий нет), а другому – проигрыш как больше, так и меньше цены игры.