Если число стратегий одного из игроков равно двум, то для нахождения оптимальных стратегий можно легко воспользоваться графическим методом.
Пусть платежная матрица имеет вид
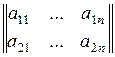 .
.
Для произвольной стратегии второго игрока, контролирующего столбцы, имеем выигрыш первого игрока
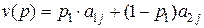 ,
,
поскольку, как сказано раньше,
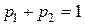 ,
, 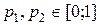 .
.
Графиком зависимости 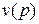 будет некоторая прямая. Для разных стратегий, то есть для разных
будет некоторая прямая. Для разных стратегий, то есть для разных 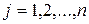 , получаются разные прямые.
, получаются разные прямые.
На рис. 6.1 изображен случай 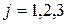 для игры 2
для игры 2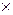 3. Из принципа минимакса следует, что надо взять нижнюю огибающую всех прямых, соответствующих стратегиям второго игрока (она показана на рисунке жирной линией), а на этой ломаной, обязательно обращенной выпуклостью вверх, надо найти вершину, имеющую максимальное значение v*. Абсцисса этой точки x * и будет искомым значением p 1 *.
3. Из принципа минимакса следует, что надо взять нижнюю огибающую всех прямых, соответствующих стратегиям второго игрока (она показана на рисунке жирной линией), а на этой ломаной, обязательно обращенной выпуклостью вверх, надо найти вершину, имеющую максимальное значение v*. Абсцисса этой точки x * и будет искомым значением p 1 *.
Геометрически можно определять и оптимальную стратегию игрока В для игры 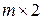 , но в этом случае строится не нижняя, а верхняя граница выигрыша и на ней определяется не максимум, а минимум.
, но в этом случае строится не нижняя, а верхняя граница выигрыша и на ней определяется не максимум, а минимум.
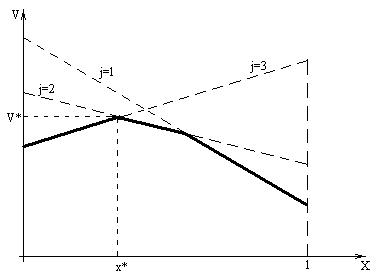
Рис. 6.1. Графическое нахождение цены игры
Пример 6.4. Решить графически игру, заданную платежной матрицей: 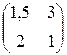
Для игрока А решение представлено на рис. 6.2. Находя точку пересечения соответствующих прямых, получаем N (0,6; 1,8).
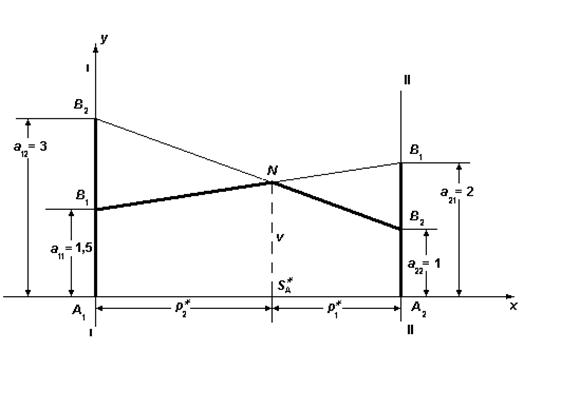
Рис. 6.2. Решение матричной игры для игрока А
Следовательно, оптимальная стратегия игрока А заключается в выборе стратегии А 1 с вероятностью 0,6 и стратегии А 2 с вероятностью 0,4 = 1 – 0,6. При этом цена игры v = 1,8.
Для игрока В решение представлено на рис. 6.3. Находя точку пересечения соответствующих прямых, получаем М(0,2; 1,8).
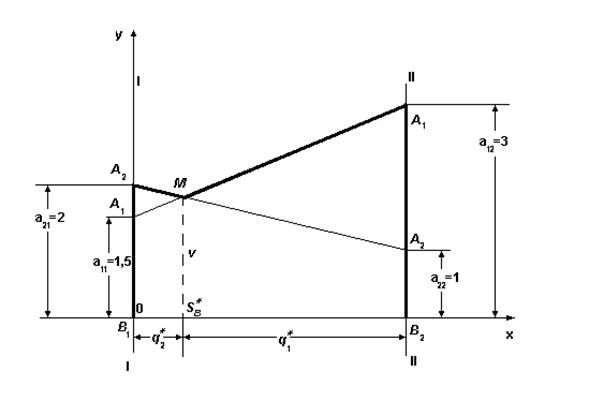
Рис. 6.3. Решение матричной игры для игрока В
Следовательно, оптимальная стратегия игрока В заключается в выборе стратегии В 1 с вероятностью 0,8 и стратегии В 2 с вероятностью
0,2 = 1 – 0,8.
Оптимальное решение игры найдено.
 2014-02-12
2014-02-12 764
764








