Программирования

Приведение матричной игры к задаче линейного

Пусть имеем игру размерности 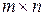с матрицей

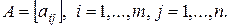
Обозначим через р *= 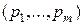, q * =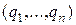оптимальные смешанные стратегии игроков А и В. Стра­тегия р * игрока А гарантирует ему выигрыш не меньше v, независимо от выбора стратегии В_j игроком В. Это можно записать так:

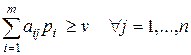, (6.7)

где .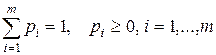

Аналогично стратегия q * игрока В гарантирует ему проигрыш не больше v, независимо от выбора стратегии А_i игроком А, т. е.

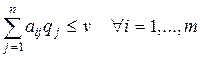, (6.8)

где .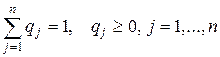

Поскольку элементы платежной матрицы на основании теоремы 6.5 всегда можно сделать положительными, то и цена игры v > 0.

Преобразуем системы (6.7) и (6.8), разделив обе части каждого неравенства на положительное число v, и введем новые обозначения

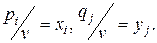
Получим:

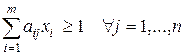, где 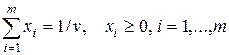, (6.9)

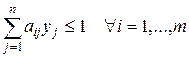, где 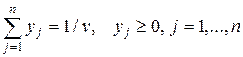. 6.10)

Так как игрок А стремится максимизировать цену игры v, то обратная величина 1/ v будет минимизироваться, по­этому оптимальная стратегия игрока А определится из ЗЛП следующего вида: найти минимальное значение функции 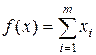при ограничениях (6.9).

Оптимальная смешанная стратегия игрока В опреде­лится решением задачи следующего вида: найти макси­мальное значение функции 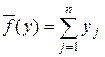при ограничениях (6.10).

Решив пару двойственных задач графическим (для случая двух переменных) или симплексным методом, да­лее определим:

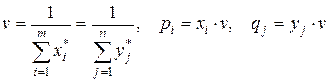. (6.11)

Проиллюстрируем решение матричной игры сведением ее к ЗЛП.

Пример 6.5. Найти оптимальное решение игры, заданной платежной матрицей:

.

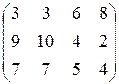Прежде чем решить игру, можно попытаться ее упростить, проведя анализ платежной матрицы и отбросив стратегии, заведомо невыгодные или дублирующие. Так, вторая стратегия игрока В является заведомо невыгодной по сравнению с первой (элементы второго столбца матрицы не меньше соответствующих элементов первого столбца), т.к. цель В – уменьшить выигрыш А. Поэтому эту стратегию можно отбросить.

Получим новую матрицу:

.

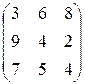Определим верхнюю и нижнюю цену игры в таблице 6.2.

Таблица 6.2

	В1	В2	В3
А1
А2
А3

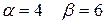
Так как 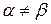, седловая точка отсутствует. Следовательно, оптимальное решение нужно искать в смешанных стратегиях:

.

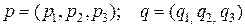Обозначив 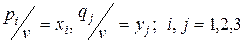, составим две взаимно-двойственные задачи линейного программирования:

Задача 1

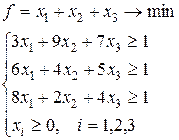
Задача 2

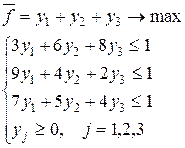
Введя дополнительные переменные и решая вторую из этих задач симплекс-методом, находим оптимальное решение:

.

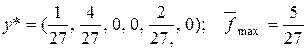На основании теорем двойственности находим решение задачи 1:

.

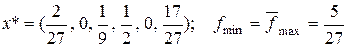Из соотношений (6.11) находим:

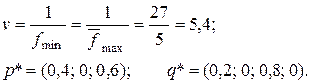
(При нахождении q * было учтено, что второй столбец отброшен как невыгодный.)

Таким образом, при решении произвольной конечной игры размера т ´ п рекомендуется придерживаться следующей схемы:

1. Исключить из платежной матрицы заведомо невыгодные стратегии по сравнению с другими стратегиями. Такими страте­гиями для игрока А (игрока В) являются те, которым соответству­ют строки (столбцы) с элементами, заведомо меньшими (боль­шими) по сравнению с элементами других строк (столбцов).

2. Определить верхнюю и нижнюю цены игры и проверить, имеет ли игра седловую точку. Если седловая точка есть, то соответствующие ей стратегии игроков будут оптимальными, а цена совпадает с верхней (нижней) ценой.

3. Если седловая точка отсутствует, то решение следует искать в смешанных стратегиях. Для игр размера т ´ п рекомендуется симплексный метод, для игр размера 2 ´ 2, 2 ´ п, т ´ 2 возможно геометрическое решение.