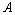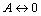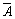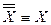Опр. Две булевы формулы называются эквивалентными(равносильными), если при всех наборах значений входящих в них переменных эти формулы принимают одинаковые значения истинности.
Т.е. если таблицы истинности двух булевых формул совпадают, то эти формулы эквивалентны и определяют одну и ту же булеву функцию.
Построение таблиц истинности для сложных выражений:
Количество строк = 2n + две строки для заголовка (n - количество простых высказываний)
Количество столбцов = количество переменных + количество логических операций
Алгоритм построения таблицы истинности
1. Определить число переменных
2. Определить число строк в таблице истинности
3. Записать все возможные значения переменных
4. Определить количество логических операций и их порядок
5. Записать логические операции в таблицу исинности и определить для каждой значение
Задача 1. Используя таблицы истинности, проверить эквивалентность следующих булевых формул.
 x
x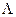 y
y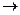 z
z 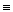 x
x 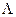
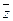
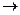
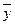

Для выполнения данного задания нужно знать то, какие формулы считаются эквивалентными. Существует два способа доказательства равносильности формул – с помощью равносильных преобразований и по таблицам истинности. В данном задании от нас требуется установить эквивалентность формул на основании их таблиц истинности.
Составим сводную таблицу истинности для данных формул (в наших обозначениях мы придерживаемся следующей символики: 1 – истина, 0 - ложь):
| x | y | z | x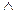 y y | F1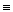 x x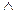 y y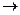 z z | 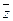 | x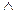 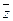 | 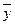 | F2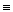 x x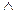 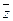 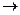 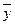 |
Т.к. результативные столбцы для формулы F1 и F2 в таблице истинности совпадают, то данные формулы эквивалентны.
Замечание2.
В данном случае функции заданы аналитически (с помощью формулы), поэтому порядок заполнения комбинаций наборов значений переменных, входящих в формулы, не важен, т.к. последовательно выполняя все действия, мы однозначно получим результативный столбец. В случае же, когдазадается с помощью вектора значений (те. дан результативный столбец), произвольное заполнение столбцов, определяющих значения переменных, может при вести к неоднозначному результату при выполнении задания.
Договоримся о том, что в дальнейшем для однозначности при составлениитаблицы истинностидля какой-либоформулыкомбинации наборовзначений переменных, от которых зависитэта формула, будем заполнять именно втакомпорядке, как мы указали в приведенной выше таблице.
2. Тождественность формул ЛВ. Основные тождества ЛВ
| Определение 1 | |||||||||
Высказывания 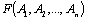 и и 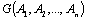 называются равносильными (или просто равными), если для любых наборов называются равносильными (или просто равными), если для любых наборов 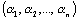 имеет место равенство: имеет место равенство: 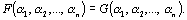 Обозначим Обозначим 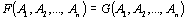 . Другими словами, два высказывания равны, если у них совпадают таблицы истинности. . Другими словами, два высказывания равны, если у них совпадают таблицы истинности. | |||||||||
| Примеры | |||||||||
1) 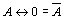 . . | |||||||||
| Доказательство | |||||||||
|
Основные логические тождества
1. XºX Закон тождества.
2. 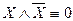 Закон противоречия
Закон противоречия
3. 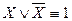 Закон исключенного третьего
Закон исключенного третьего
5. XÙXºX ý Законы идемпотентности
XÚXºC
6. CÙUºUÙC } Законы коммутативности
CÚUºUÚC (переместительности)
7. (CÙU)ÙZºCÙ(UÙZ) } Законы ассоциативности
(CÚU)ÚZºCÚ(UÚZ) (сочетательности)
8. CÙ(UÚZ)º(CÙU)Ú(CÙZ) } Законы дистрибутивности
CÚ(UÙZ)º(CÚU)Ù(CÚZ) (распределительности)
9. 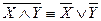 } Законы де Моргана
} Законы де Моргана
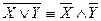
10. XÙ1ºC CÚ0ºC
11. CÙ0º0; CÚ1º1
12. CÙ(CÚU)ºC } Законы поглощения
CÚ(CÙU)ºC
13. (CÚU)Ù(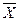 ÚU)ºU } Законы склеивания
ÚU)ºU } Законы склеивания
(CÙU)Ú(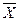 ÚU)ºU
ÚU)ºU
14. 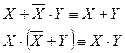
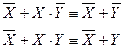
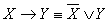
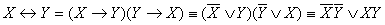
Закон контрапозиции: прямое предложение равносильно обратно противоположному.
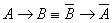
3. СДНФ
4. СКНФ
5. Составление СДНФ с помощью таблиц истинности
6. Составление СКНФ с помощью таблиц истинности
Опр. Элементарной конъюнкцией (дизъюнкцией) называется формула, если она представляет собой соответственноконъюнкцию (дизъюнкцию) переменных и их отрицаний.
Опр. ДНФ (дизъюнктивной нормальной формой) называется формула,котораяпредставляет собой дизъюнкцию элементарных конъюнкций.
Опр. КНФ (конъюнктивной нормальной формой) называется формула,которая представляет собой конъюнкцию элементарных дизъюнкций.
Опр. СДНФ (совершенной дизъюнктивной нормальной формой) для булевой функции F (x1, x2,…, xn ), не равной тождественно 0, называется такаяформула:
), не равной тождественно 0, называется такаяформула:
1) которая является ДНФ;
2)среди элементарных конъюнкций, входящих в нее, нет одинаковых;
3) каждая элементарная конъюнкциясодержит все переменные, от которыхформула зависит, и каждая элементарная конъюнкция содержит ровно n элементов, где n -число переменных, от которых зависит формула.
В аналогичнойформе дадим определение СКНФ.
Опр. СКНФ (совершенной конъюнктивной нормальной формой) для булевой функции F (x1, x2,…, xn ), не равной тождественно 1, называется такаяформула:
), не равной тождественно 1, называется такаяформула:
1) которая является КНФ;
2)среди элементарных дизъюнкций, входящих в нее, нет одинаковых;
3) каждая элементарная дизъюнкциясодержит все переменные, от которыхформула зависит, и каждая элементарная дизъюнкция содержит ровно n элементов, где n -число переменных, от которых зависит формула.
Существует два способа построения СДНФ и СКНФ - с помощью равносильных преобразований и по таблице истинности. В данном случае нас интересует алгоритм построения СДНФ и СКНФ по таблице истинности.
Алгоритм построения СДНФ по таблице истинности:
1. Выбираем строки,где функция принимает значение 1;
2. Покаждой строке строим элементарные конъюнкции из переменных,
откоторых зависит формула, следующим образом:
- если переменная встроке принимает значение 1, то она непосредственно в неё входит;
- если же значение 0, то она входит в нее с отрицанием.
3. Из данных элементарных конъюнкций строим ДНФ, в результате получаем СДНФ.
Алгоритм построения СКНФ по таблице истинности:
1. Выбираем строки,где функция принимает значение 0;
2. Покаждой строке строим элементарные дизъюнкции из переменных,
откоторых зависит формула, следующим образом:
- если переменная встроке принимает значение 0, то она непосредственно в неё входит;
- если же значение 1, то она входит в нее с отрицанием.
3. Из данных элементарных дизъюнкций строим КНФ, в результате получаем СКНФ.
Задача 2. Для булевой функции F(01010101), заданной вектором значений,определить: 1) СДНФ
Решение:
Выполнение этого задания начнем с построения таблицы истинностидля функции.
| x | y | z | F(x, y, z) |
Итак, перейдем к выполнению обозначенных пунктов нашего задания.
1) Построим СДНФ для заданной булевой функции F = (01010101). Выбираем четные строки в нашей таблице, где функция принимает значение 1.
Строим элементарные конъюнкции:
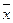
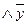
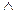 z (2) x
z (2) x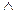
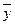
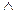 z (6)
z (6)
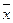
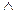 y
y 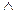 z (4) x
z (4) x 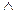 y
y 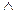 z (8)
z (8)
Из данных элементарных конъюнкций строим ДНФ, котораяудовлетворяет всем условиям в определении СДНФ:
(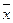
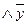
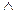 z)
z)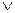 (
(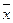
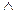 y
y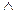 z)
z) 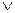 (x
(x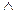
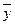
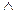 z)
z) 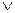 (x
(x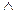 y
y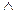 z) – СДНФ.
z) – СДНФ.
Правила приведения в СДНФ с помощью равносильных преобразований:
1) Приводим к нормальному виду
Нормальная форма логической формулы не содержит знаков импликации, эквиваленции и отрицания неэлементарных формул.
2) Из всех одинаковых членов дизъюнкции оставляем только один
3) Если в каком-то слагаемом не хватает переменной x0, то домножаем на 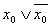
4) Раскрываем скобки
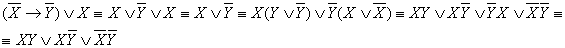
Правила приведения в СКНФ:
1) Приводим к нормальному виду
2) Из всех одинаковых членов конъюнкции оставляем только один
3) Если в каком-то слагаемом не хватает переменной x0, то прибавляем 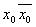
4) Раскладываем на множители
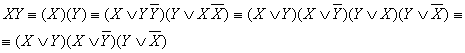
7. Булевы функции, фиктивные и существенные переменные, полином Жегалкина
 2014-02-12
2014-02-12 1334
1334