Определение 1: Переменная x, принимающая значения из {0,1}, называется булевой переменной(логической, двоичной). Двоичные переменные используются в двоичной системе счисления для передачи данных.
Булева функция - функция, аргументы которой, равна как и сама функция, принимают значения из двух элементного множества {0,1}. Уменьшить это множество до одногоэлементного нельзя, так как произойдет вырождение понятия функции. Таким образом булевы функции занимают первую ступень в иерархии функций.
Опр. Переменная xiбулевой функции F (х1,…,хi-1, хi, хi+1,…,хn ) называется фиктивной если при любых наборах значений переменных х1,…,хi-1, хi, хi+1,…,хn имеет место равенство:
F (х1,…,хi-1,0,хi+1,…,хn )=F (х1,…,хi-1,1,хi+1,…,хn ).
Данные наборы значений переменных называются соседними по переменной x i. Иначе переменная хi называется существенной.
Опр. Полиномом (многочленом) Жегалкина от n переменных называетсяформула, которую можно записать в виде суммы произведений, содержащей 2n слагаемых:
G(x1,…, xn) = a0 a1 x1
a1 x1 a2 x2
a2 x2 …
… an xn
an xn an+1 x1
an+1 x1
Теорема. Любая функция от n переменных может быть представлена полиномом Жегалкина, и это представление единственно.
Пример Составим полином Жегалкина по таблице истинности для данной булевой функции F=(01010101).Запишем егосначала с неопределёнными коэффициентами:
G(x,y,z)= a0 a1x
a1x a2y
a2y a3z
a3z a4xy
a4xy a5xz
a5xz a6yz
a6yz a7xyz.
a7xyz.
Подставим в него по очереди вместо переменных х, у,z все 8наборових значений, каждый раз приравнивая сумму к значению функции F(х, у,z) в соответствующей строке, тем самымполучим 8 уравнений, из которых и найдём коэффициенты полинома Жегалкина.
x = 0, y = 0, z = 0: a0 = 0;
x = 0, y = 0, z = 1: a0  a3= 1
a3= 1  a3= 1;
a3= 1;
x = 0, y = 1, z = 0: a0  a2= 0
a2= 0  a2= 0;
a2= 0;
x = 0, y = 1, z = 1: a0  a2
a2  a3
a3 a6= 1
a6= 1  a6= 0;
a6= 0;
x = 1, y = 0, z = 0: a0  a1= 0
a1= 0 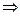 a1= 0;
a1= 0;
x = 1, y = 0, z = 1: a0  a1
a1 a3
a3 a5= 1
a5= 1 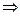 a5= 0;
a5= 0;
x = 1, y = 1, z = 0: a0  a1
a1 a2
a2 a4= 0
a4= 0 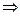 a4= 0;
a4= 0;
x = 1, y = 1, z = 1: a0  a1
a1 a2
a2 a3
a3 a4
a4 a5
a5 a6
a6 a7= 1
a7= 1 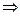 a7= 0.
a7= 0.
Т.е.полином Жегалкина для данной функции имеет вид: G(х. у, z) =z
(причем, очевидно, переменные х и у для даннойфункции являются фиктивными).
8. Классы функций
9. Замыкания множеств, замкнутые множества
Пусть имеется некоторый набор К, состоящийизконечного числа булевых функций.
Опр. Суперпозициейфункций из набора К называются новые функции,полученные с помощью конечного числа применения следующих операций:
1) можно переименовать любую переменную, входящую в функцию из набора К; 2) вместо любой переменной можно поставитьфункцию из набора К.
или уже образованную ранее суперпозицию. Суперпозицию еще иначе называют сложной функцией.
Опр. Система булевых функций f1, f2,…, fn называется функционально полной, если любая булева функция может быть представлена суперпозицией функции данной системы.
Перейдем теперь к выяснению полноты конкретных наборов функций. Для этого перечислим 5 важнейших классов функций:
1. К0 – это класс функций, сохраняющих 0 (т.е. это набор всехтех логических функций,которые на нулевом наборе принимают значение 0);
2. К1 - это класс функций, сохраняющихединицу (т.е. это набор всехлогических функций, которые на единичном наборе принимают значение 1);
3. КлассКс - класс самодвойственных функций.
Функция f (x1, x2,…, xn ) называетсясамодвойственной, если на противоположных наборах значений переменных она принимает противоположные значения, т.е. самодвойственная функция f (x1, x2,…, xn ) удовлетворяет условию: f (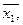
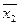 , …,
, …, 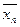 ) =
) = 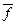 ( x1, x2,…, xn ).
( x1, x2,…, xn ).
4. КМ - класс монотонных функций.
Опишем класс этих функций более подробно.Пусть даны следующиедва двоичных набора от n переменных: s1 = (x1, x2,…, xn) и s2 = (y1, y2,…, yn).
Будем говорить, что s1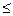 s2,. если все xi
s2,. если все xi 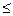 yi.
yi.
Функция f (x1, x2,…, xn ) называется монотонной, если длялюбых двоичных наборов длины n s1 и s2 из того, что s1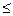 s2, следует, что f (s1)
s2, следует, что f (s1) 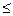 f (s2).
f (s2).
Разумеется, эти неравенства должны проверяться только на сравнимых наборах. Понятно, что несравнимые наборы - это те, в которых есть некоторыекоординаты типа (0,1) в одном наборе в и (1,0) в другомна соответствующих местах.
5. КЛ - класс линейных функций, т. е. такие функции, которые представляются полиномом Жегалкина первой степени. Т.е. функция, у которой полиномЖегалкина имеет вид 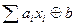 , где аi, b Î {0,1}, называется линейной.
, где аi, b Î {0,1}, называется линейной.
Опр. Система булевых функций К называется замкнутым классом, если любая суперпозиция функций из К снова принадлежит К.
Теорема.
Классы функций К0,К1,КС,КМ,КЛ замкнуты.
Принадлежность булевой функции замкнутым классам (1 - 4) проверяется по таблице истинности, а классу (5) – с помощью построения полинома Жегалкина.
10. Теорема Поста-Яблонского. Выводы из этой теоремы.
Теорема Поста.
Для того чтобы система булевых функций была функционально полной, необходимо и достаточно, чтобы она содержала:
1) нелинейную функцию;
2) немонотонную функцию;
3) несамодвойственную функцию;
4) функцию, не сохраняющую 0;
5) функцию, не сохраняющую 1.
Из этойтеоремы следует довольно простой способ выяснения полноты некоторого набора функций. Длякаждой изэтих функций выясняется принадлежностьк перечисленным выше классам. Результаты заносятся в так называем у ю таблицу Поста (причем знаком“+“ отмечается принадлежностьфункции соответствующему классу, знак “-”означает, что функция в него невходит). В соответствии с теоремой Поста набор функций будет полным тогда и только тогда, когда в каждом столбце таблицы Поста имеется хотя быодни минус.
Задача З. Выяснить, является ли следующая система функций функционально полной:
A={F1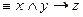 , F2
, F2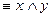 , F3
, F3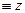 , F4
, F4 1, F5
1, F5 0}.
0}.
Используя данные теоретические сведения, перейдем к непосредственному выяснению полноты заданной системы функций А.
1) Исследуем функцию F1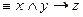 — на принадлежность указаннымклассам. Таблица истинности данной функции была нами построена в задании 1.
— на принадлежность указаннымклассам. Таблица истинности данной функции была нами построена в задании 1.
· F1 (0,0,0) = 1Þ F1(x,y,z)ÏK0
· F1 (1,1,1) = 1Þ F1(x,y,z)ÎK1
· F1 (0,0,0) = F1 (1,1,1) Þ F1(x,y,z)ÏKC
· Из того, что (0,0,0)£(1,1,0)Þ F1 (0,0,0) =1> F1 (1,1,0)=0, значит, F1(x,y,z) ÏKМ
· Построим полином Жегалкина для данной функции. В результате
последовательной подстановки вместо переменных всех комбинаций значений в общий вид полинома Жегалкина от 3-хпеременныхG(х, у, z)=a0 Å a1x Å a2y Å a3z Å a4xy Å a5xz Å a6yzÅ a7xyz, получим, что a0=1, a1=0, a2=0, a3=0, a4=1, a5=0, a6=0, a7=1
Таким образом, полином Жегалкина для функции F1ºxÙy® z имеет вид:
G(x,y,z)= xyz Å xy Å 1.Очевидно, что данный полином не выражаетсялинейной функцией, т.е.F1(x,y,z)ÏKЛ.
2) Теперь исследуем функцию F2ºxÙy. Воспользуемся все той же таблицей истинности из задания 1, где также определена данная функция.
· F2(0,0)=0Þ F2(x,y) Î K0
· F2(1,1)=1Þ F2(x,y)Î K1
· F2(1,0)= F2(0,1)Þ F2(x,y)Ï KC
· Из того, что (0,0) £ (1,0)Þ F2(0,0)=0 £ F2(1,0)=0; (0,0) £ (0,1)Þ F2(0,0)=0 £ F2(0,1)=0;
(0,0) £ (1,1)Þ F2(0,0)=0 £ F2(1,1)=1;
Значит, F2(x,y,z) Î KM.
· Найдем полином Жегалкина для, данной функции. Выполнив всенеобходимые действия, в итоге получим, что а0=0, а1=0, а2=0, а3=0, а4=1, а5=0, а6=0, а7=0.
·
Таким образом, полином Жегалкина для функции F2ºxÙyвыражается ввиде самой функции: G2(x,y) = xy Þ F2(x,y,z)ÏKЛ.
3) Дляфункций F3,F4,F5 подробное исследование проводить не будем всилу его очевидности. Всеполученные результаты занесем в соответствующие строкитаблицыПоста.
| K0 | K1 | KС | KМ | KЛ | |
| F1 | - | + | - | - | - |
| F2 | + | + | - | + | - |
| F3 | + | + | + | + | + |
| F4 | - | + | - | + | + |
| F5 | + | - | - | + | + |
Итак, вкаждом столбце таблицы Поста есть хотябы один “-“‚ значит, системафункций являетсяфункционально полной.
11. Минимизация булевых функций с помощью карты Карно.
Поясним, что карта Карно - это схематическое представление булевой
функции в виде дизъюнктивной формы. Карта состоит из прямоугольника, который разбивает на клетки. Для заданного числа переменных, от которых зависит функция, все клетки карты Карно представляют собойвсевозможные слагаемые, которые участвуют в СДНФ.Эти слагаемые располагаются в клетках карты таким образом, чтобы ближайшие соседние клетки(кроме диагональных) содержали слагаемые., которые отличаются друг отдруга одним сомножителем и каждый раз новым. Требование для слагаемых
“отличаться друг от друга одним сомножителем и каждый раз новым” также
выполняется и для границ карты. Здесь имеетсяв виду возможность “сшивания границ”, при которой последняя правая колонка карты становится предшествующей первой левой колонке, а также верхняя строка считаетсяпоследующей за нижнейстрокой.
Задача 2. Для булевой функции F(01010101), заданной вектором значений,определить: 1) СДНФ, которую затем минимизировать по карте Карно
Сднф мы уже получили (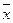
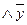
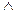 z)
z)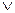 (
(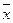
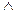 y
y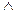 z)
z) 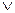 (x
(x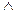
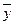
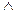 z)
z) 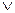 (x
(x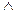 y
y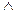 z)
z)
Составим теперь для данной функции Fкарту Карно,с помощью которой мы минимизируем (сократим) найденную СДНФ.
Существуют различные способы конструирования карт Карно ( см. указанную литературу), одним из которых мы сократим полученнуюнами СДНФ. Вклетку карты мы будем вписывать 1,если на пересечении соответствующего столбца и строки стоят сомножители слагаемого, которое присутствуетв СДНФ. Если же какое-либо слагаемое отсутствует, то клетку оставляемпустой.
Заполним карту Карно для даннойфункции F от 3-хпеременных.
yz 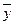 z
z 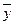
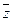 y
y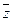
x
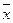
Напомним, что карты Карно предназначены для минимизации булевых функций.
Приведем правило минимизации булева выражения:
1. Изолируем все единицы, которые не имеют ближайших соседей— единиц. Слагаемые, отвечающие таким единицам, не упрощаются.
2. Выделяем те единицы, которые имеют только по одной соседнейклетке,содержащей единицу, т.е. блок из 2-х соседних единиц. Такие пары заменяем слагаемыми, которые содержат в качестве сомножителей элементы, общие для обеих клеток.
3.Выделяем те единицы, которые могут быть объединены в блок из 4-х соседних единиц. Такие блоки соответствуют слагаемым, которые содержат в качестве сомножителей элементы, общие для всех четырех клеток.
4.Выделяем те единицы, которые могут быть локализованы в блок из 8-ми соседних единиц. Ихмы заменяем слагаемыми, которые содержат в качестве сомножителей элементы, общие для всех восьми клеток.
5. Оставшиеся единицы по возможности присоединяем к выделенным блокам.
Действуем в соответствии с нашим правилом.
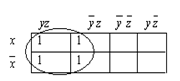
Вданном случае изолированных единиц нет, групп только из 2-х соседних единиц также нет, поэтому мы обводим кружком блок из 4-х соседнихединиц. Заменяем его одним слагаемым, состоящим из элементов, общих для всех четырех клеток, те.z.
Таким образом, мы сократили полученную нами СДНФ для данной функции F(x,y,z) по карте Карно, те. минимизированная форма имеет следующий вид: F(x,y,z) = z.
12. Множества. Операции над множествами (объединение, пересечение, вычитание, дополнение)
Множество - это совокупность объектов, рассматриваемая как одно целое. Понятие множества принимается за основное, т. е. не сводимое к другим понятиям. Объекты, составляющие данное множество, называются его элементами. Основное отношение между элементом a и содержащим его множеством A обозначается так 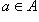 (a есть элемент множества A; или a принадлежит A, или A содержит a). Если a не является элементом множества A, то пишут
(a есть элемент множества A; или a принадлежит A, или A содержит a). Если a не является элементом множества A, то пишут 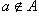 (a не входит в A, A не содержит a). Множество можно задать указанием всех его элементов, причем в этом случае употребляются фигурные скобки. Так { a, b, c } обозначает множество трех элементов. Аналогичная запись употребляется и в случае бесконечных множеств, причем невыписанные элементы заменяются многоточием. Так, множество натуральных чисел обозначается {1, 2, 3,...}, а множество четных чисел {2, 4, 6,...}, причем под многоточием в первом случае подразумеваются все натуральные числа, а во втором - только четные.
(a не входит в A, A не содержит a). Множество можно задать указанием всех его элементов, причем в этом случае употребляются фигурные скобки. Так { a, b, c } обозначает множество трех элементов. Аналогичная запись употребляется и в случае бесконечных множеств, причем невыписанные элементы заменяются многоточием. Так, множество натуральных чисел обозначается {1, 2, 3,...}, а множество четных чисел {2, 4, 6,...}, причем под многоточием в первом случае подразумеваются все натуральные числа, а во втором - только четные.
Два множества A и B называются равными, если они состоят из одних и тех же элементов, т. е. если каждый элемент множества A принадлежит B и, обратно, каждый элемент B принадлежит A. Тогда пишут A = B. Таким образом, множество однозначно определяется его элементами и не зависит от порядка записи этих элементов. Например, множество из трех элементов a, b, c допускает шесть видов записи:
{ a, b, c } = { a, c, b } = { b, a, c } = { b, c, a } = { c, a, b } = { c, b, a }.
Из соображений формального удобства вводят еще так называемое "пустое множество", а именно, множество, не содержащее ни одного элемента. Его обозначают 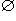 , иногда символом 0 (совпадение с обозначением числа нуль не ведет к путанице, так как смысл символа каждый раз ясен).
, иногда символом 0 (совпадение с обозначением числа нуль не ведет к путанице, так как смысл символа каждый раз ясен).
Если каждый элемент множества A входит во множество B, то A называется подмножеством B, а B называется надмножеством A. Пишут 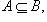
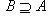 (A входит в B или A содержится в B, B содержит A). Очевидно, что если
(A входит в B или A содержится в B, B содержит A). Очевидно, что если 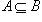 и
и 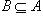 , то A = B. Пустое множество по определению считается подмножеством любого множества.
, то A = B. Пустое множество по определению считается подмножеством любого множества.
Если каждый элемент множества A входит в B, но множество B содержит хотя бы один элемент, не входящий в A, т. е. если 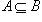 и
и 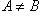 , то A называется собственным подмножеством B, а B - собственным надмножеством A. В этом случае пишут
, то A называется собственным подмножеством B, а B - собственным надмножеством A. В этом случае пишут 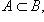
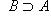 . Например, запись
. Например, запись 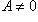 и
и 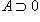 означают одно и то же, а именно, что множество A не пусто.
означают одно и то же, а именно, что множество A не пусто.
Заметим еще, что надо различать элемент a и множество { a }, содержащее a в качестве единственного элемента. Такое различие диктуется не только тем, что элемент и множество играют неодинаковую роль (отношение 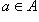 не симметрично), но и необходимостью избежать противоречия. Так, пусть A = { a, b } содержит два элемента. Рассмотрим множество { A }, содержащее своим единственным элементом множество A. Тогда A содержит два элемента, в то время как { A } - лишь один элемент, и потому отождествление этих двух множеств невозможно. Поэтому рекомендуется применять запись
не симметрично), но и необходимостью избежать противоречия. Так, пусть A = { a, b } содержит два элемента. Рассмотрим множество { A }, содержащее своим единственным элементом множество A. Тогда A содержит два элемента, в то время как { A } - лишь один элемент, и потому отождествление этих двух множеств невозможно. Поэтому рекомендуется применять запись 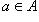 , и не пользоваться записью
, и не пользоваться записью 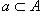 .
.
Объединением множеств A и B называется множество элементов, принадлежащих по крайней мере одному из данных множеств (т. е. либо A, либо B, либо одновременно и A и B). Обозначают 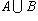 и читают "объединение A и B ".
и читают "объединение A и B ".
Пересечением множеств A и B называется множество элементов, принадлежащих одновременно и A и B. Обозначают 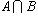 и читают "пересечение A и B ".
и читают "пересечение A и B ".
Разностью множеств A и B называется множество элементов, принадлежащих A и не принадлежащих B. Обозначают A \ B и читают "разность A и B ".
Пример 1. Пусть A есть отрезок [1, 3], B - отрезок [2, 4]; тогда объединением 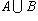 будет отрезок [1, 4], пересечением
будет отрезок [1, 4], пересечением 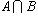 - отрезок [2, 3], разностью A \ B - полуинтервал [1, 2), B \ A - полуинтервал (3, 4].
- отрезок [2, 3], разностью A \ B - полуинтервал [1, 2), B \ A - полуинтервал (3, 4].
Пример 2. Пусть A есть множество прямоугольников, B - множество всех ромбов на плоскости. Тогда 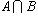 есть множество всех квадратов, A \ B - множество прямоугольников с неравными сторонами, B \ A - множество всех ромбов с неравными углами.
есть множество всех квадратов, A \ B - множество прямоугольников с неравными сторонами, B \ A - множество всех ромбов с неравными углами.
Операции объединения и пересечения множеств обладают многими свойствами сложения и умножения чисел, например переместительным, сочетательным и распределительным свойствами.
Понятия объединения и пересечения множеств дословно переносятся на случай более двух множеств и даже на случай любого конечного или бесконечного множества множеств.
Для удобства будем называть системами такие множества, элементами которых служат другие множества. Тогда объединением множеств некоторой системы называется множество, состоящее из элементов, принадлежащих по крайней мере одному множеству данной системы. Пересечением множеств некоторой системы называется множество, состоящее из элементов, входящих во все множества данной системы.
Применяются следующие обозначения. В случае конечной системы множеств A 1, A 2,..., An объединение S и пересечение D обозначаются:
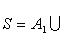
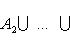



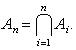
13. Декартово произведение множеств
Определение. Декартовым (прямым) произведением множеств А и В (обозначение AxB) называется множество всех упорядоченных пар (a;b), таких, что aEA, bEB. В частности, если А=В, то обе координаты принадлежат множеству А, такое произведение обозначается А2. Аналогично, прямым произведением множеств A1, A2,... An называется множество всех векторов (a1, a2,... an) длины п, таких, что a1EA1,a2EA2... anEAn.
например даны множества A={1,2,3} и B={a,b} их декартово произведение A × B ={(1,a),(1,b),(2,a),(2,b),(3,a),(3,b)}
14. Соответствия (область отправления, область прибытия, область определения, область значений, образ, прообраз). Примеры.
15. Виды соответствий (инъективное, сюръективное, всюдуопределенное, функциональное соответствие).
Понятие соответствия
Пусть заданы два множества X и Y. Если для каждого элемента x∈X
указан элемент y∈Y, с которым сопоставляется x, то говорят, что между
множествами X и Y установлено соответствие. Иначе говоря, соответствием
называется тройка множеств Г=(X,Y,G), где G⊂X×Y. Множество X
называется областью отправления, Y – областью прибытия, G – графиком
соответствия. Если (x,y)∈G, то множество первых проекций (Пр1G)
называется областью определения соответствия, множество вторых проекций
(Пр2G) – областью значений этого соответствия, G – графиком
соответствия.
Два соответствия равны, тогда и только тогда, когда равны их области
отправления, области прибытия и графики.
В соответствии (X,Y,G) множество всех y∈Y, которые сопоставляются
элементу x∈X, называется образом x в Y.
Множество же всех x∈X, которым сопоставляют элемент y∈Y, называется
прообразом y в X.
Соответствие называется всюду определенным, если множество Пр1G=X,
то есть его область определения совпадает с областью отправления (в
противном случае говорят о частичном соответствии). Если же Пр2G=Y, то
соответствие называют сюръективным, или накрывающим. Это означает, что
область значений соответствия совпадает с его областью прибытия.
Соответствие (X,Y,G) называется функциональным (или однозначным),
если образом любого элемента из Пр1G является единственный элемент из
Пр2G. График такого соответствия называется функциональным. Это
означает, что в нем нет пар с одинаковыми первыми и различными вторыми
компонентами. Соответствие называется инъективным, если любому
элементу из Пр2G соответствует единственный элемент из Пр1G
Соответствие между X и Y называется взаимно-однозначным (или
биективным), если оно всюду определено, сюръективно, функционально и
инъективно.
16. Графы – основные определения (граф, ориентарованный и неориентированный граф, смежность вершин и ребер, инцидентность ребра вершине, полный граф, простой граф, изоморфизм графов, маршрут)
Наглядное представление о графе можно получить, если представить себе некоторое множество точек плоскости Х, называемых вершинами, и множество направленных или ненаправленных отрезков М, соединяющих все или некоторые из вершин и называемых дугами. Математически граф определяется как пара множеств (Х, Г).
Определение: Если две вершины соединены направленным отрезком, то пара называется упорядоченной, а отрезок называется ребром графа. Если вершины соединены ненаправленным отрезком, то вершины называются неупорядоченными, отрезок, их соединяющий, называется дугой.
Определение: Граф, содержащий только ребра, называется ориентированным.
Определение: Граф, содержащий только дуги, называется неориентированным.
Определение: Пара вершин может соединяться двумя или более ребрами одного направления, такие ребра называются кратными.
Определение: Дуга или ребро может начинаться или заканчиваться в одной вершине, такие дуги называются петлями. Считается, что длина петли равна 1.
Определение: Вершины, соединенные ребром или дугой называются смежными,
Определение: Дуги, имеющие общие вершины называются смежными.
Определение: Ребро и любая из двух ее вершин называется инцидентными.
17. Способы задания графов (матрица смежности и инцидентности)
Существуют различные способы задания графов. Пусть u1… un — вершины графа, а e1… em — его ребра.
1. Матрица смежности. Это матрица, размерностью nxm, такая что, Aij — равен числу ребер или дуг, соединяющую i — тую и j- тую вершины, и равна 0 если вершины несмежны.
2. Матрица инцидентности. Bij =1, если ui инцидентна ребру ej, и = 0 если вершина и ребро неинцидентны.
3. Перечислением упорядоченных или неупорядоченных пар смежных вершин.
4. Заданием множества вершин графа, и способа отображения множества Х в множество Х.
Решим задачу по ходу давая необходимые определения.
Задача 4. Построить вПДСК неориентированный граф. Вершины:v1(0;4); v2(4;4); v3(4;0);. V4(0;0).Ребра: (v1; v2); (v2; v3); (v3; v4); (v1; v4); (v1; v3); (v2; v4); (v1; v2).Указать основные характеристики данного графа. Найти: 1) таблицу степенейвершин: 2) матрицу соседства;3)матрицу инцидентности; 4) таблицу расстояний,радиус и центр графа.
Решение:
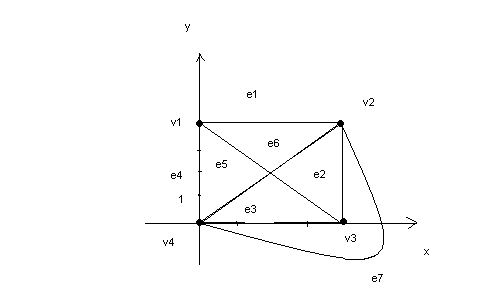
В условии задачи сказано, что данный граф — неориентированный ( что будет учтено в ниже следующих определениях). Более подробно о неориентированных графах можно узнать, например, в источнике [2].
Опр. Неориентированный граф G — это:
1) конечное множество вершин V;
2) конечное множество ребер Е;
3) функция f: E® V´V, т. е. eij®{vi,vj }.
Отметим следующие важные характеристики данного графа — он не является ни простым, ни полным, ни правильным.
Опр. Простым графом называется граф, который не имеет петель ( т.е. несодержит ребер. соединяющих вершину саму с собой) или множественных ребер (т.е. ребер, соединяющих одну и ту же пару вершин более одного раза).
Опр. Полным графом называетсяграф, у которого каждая пара различныхвершин связанаровно одним ребром.
Опр. Граф, у которого каждая вершина имеет одинаковую степень, называется правильным.
Опр. Степенью (валентностью) P(vi) вершины vi неориентированногографа G называется числоребер, исходящих из данной вершины.
Теперь переходим к выполнению всех указанных пунктов в задании.
1) Построим таблицу степеней вершин данного графа.
| vi | v1 | v2 | v3 | v4 |
| P(vi) |
Степень вершины можно определить двумя способами: непосредственно по диаграмме графа простым подсчетом исходящих ребер для каждой вершины, как мы только что выполнили, а также с помощью матрицы соседства, что мы рассмотрим далее.
 2014-02-12
2014-02-12 550
550