Поиск путей с минимальным количеством дуг

14 15 16 17 18 19 20

ЛЕКЦИЯ 23

Контрольные вопросы

Сформулировать определение орграфа. Элементы орграфа.
Понятие полустепени вершин. Теорема о количестве дуг орграфа.
Какие существуют способы задания орграфа?
Виды связностей в орграфе.
Какой подграф данного графа называется компонентой сильной связности?
Теорема о свойствах компонент сильной связности

ТЕМА: ЗАДАЧИ НА ОРИЕНТИРОВАННЫЕ ГРАФЫ

ПЛАН:

1. Поиск путей с минимальным количеством дуг

2. Минимальные пути в нагруженных орграфах

3. Порядковая функция орграфов без контуров

Главная

Путь в орграфе D(V, X) из вершины v в вершину w (v ¹ w) называется минимальным, если он имеет минимальную длину среди всех путей орграфа D из v в w.

Справедливо утверждение:

Любой минимальный путь является простой цепью.

Для решения задачи поиска минимального пути, введем обозначения:

пусть D(V,X) – граф, v Î V, V₁ Í V; обозначим D(v) = {wÎV|(v, w)Î X} – образ вершины v; D(V₁) = 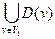- образ множества вершин V₁; D^-1(v) = { wÎV|(w, v)Î X} – прообраз вершины v; D^-1(V₁) = 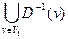- прообраз множества вершин V₁.

Пусть D(V,X) – орграф с n ³ 2 вершинами и v и w – заданные вершины из данного графа. Причем v ¹ w. Опишем алгоритм поиска минимального маршрута в графе D (алгоритм фронта волны).

Шаг1. Помечаем вершину v индексом 0. затем помечаем вершины, принадлежащие образу вершины v, индексом 1. Множество вершин с индексом 1 обозначим FW₁(v). Полагаем к =1.

Шаг 2. Если FWk(v) = Æ или выполняется к = n –1, wÏ FWk(v), то вершина w не достижима из v, и работа алгоритма на этом заканчивается. В противном случае переходим к шагу 3.

Шаг 3. Если wÏ FWk(v), то переходим к шагу 4. В противном случае существует путь из v в w длины к, и этот путь является минимальным. Последовательность вершин vw₁w₂…w_k_-1w, где

w_k_-1 Î FW_k_-1ÇD^-1(w);

w_k_-2 Î FW_k_-2ÇD^-1(w_k_-1);

……………………….

w₁ Î FW₁ÇD^-1(w₂);

и есть искомый минимальный путь из v в w.

Шаг 4. Помечаем индексом к+1 все непомеченные вершины, которые принадлежат образу множества вершин с индексом к. Множество вершин с индексом к+1 обозначим FW_k₊₁(v). Присваиваем к: = к+1 и переходим к шагу 2.

Множество FW_k(v) называют фронтом волны к- го уровня.

Замечание: Вершины w₁, w₂,…w _k_-1 могут быть выделены неоднозначно, в случае, если существует несколько минимальных путей из v в w.

Пример: Граф задан матрицей смежности:

Построим минимальный путь из u₁ в u₇. Присвоим u₁ индекс 0.

1) Составим множество образов вершины u₁ (поиск осуществляем по строкам)

FW₁ (u₁) = {u₄, u₅}. u₄ и u₅ присвоим индекс 1.

2) Ищем образы для u₄ и u₅, не включая сами эти вершины

FW₂ (u₁) = {u₆};

3) FW₃ (u₁) = {u₂, u₃}

4) FW₄ (u₁) = {u₇}.

u₇ достигнута.

Построим путь:

Каждую вершину выбираем из пересечения множеств образов с индексом k – 1 и прообразов D^-1 (u_i) с индексом k. Включаем в путь любую вершину из этого пересечения.