ТЕМА: ПОЛИНОМ ЖЕГАЛКИНА.
1. Некоторые логические операции. Двоичное сложение.
2. Полином Жегалкина.
Главная
1. Некоторые логические операции. Двоичное сложение.
Пополним список уже известных логических операций, а именно, познакомимся со штрихом Шеффера, стрелкой Пирса и операцией двоичного сложения. На последней остановимся более подробно.
Штрих Шеффера – это новое высказывание, обозначаемое х|y, ложное тогда и только тогда, когда оба высказывания х и у истинны. Приведем таблицу истинности:
| х | у | x|у |
Легко заметить, что штрих Шеффера – это отрицание конъюнкции или дизъюнкция отрицаний х и у: 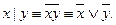 Следовательно, штрих Шеффера можно прочесть следующим образом: не х или не у.
Следовательно, штрих Шеффера можно прочесть следующим образом: не х или не у.
Используя основные равносильности, можно эту операцию выразить и через другие, например: 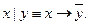
Отрицание высказывания можно представить в виде: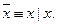
Стрелка Пирса – это новое высказывание, обозначаемое х¯ у, истинное тогда и только тогда, когда оба высказывания ложны. Приведем таблицу истинности:
| х | у | х¯у |
Стрелка Пирса – это отрицание дизъюнкции или конъюнкция отрицаний х и у:
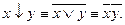
Стрелку Пирса можно прочесть так: не х и не у.
Отрицание высказывания выражается через стрелку Пирса: 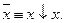
Пример: составить КНФ и ДНФ для формулы 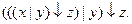
Используя новые равносильности и основные равносильности, преобразуем формулу:
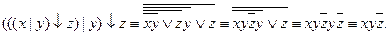 Полученная формула является одновременно ДНФ и КНФ.
Полученная формула является одновременно ДНФ и КНФ.
Двоичное сложение – это новое высказывание, обозначаемое х+у, ложное тогда и только тогда. Когда оба высказывания имеют одинаковые логические значения. Приведем таблицу истинности:
| х | у | х +у |
Двоичное сложение – это отрицание эквиваленции: 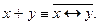
Познакомимся с законами для двоичного сложения:
1. коммутативность: х+у º у+х;
2. ассоциативность: х+у+z º x+(y+z);
3. дистрибутивность: x(y+z) º xy +xz;
4. х+0 º х;
5. 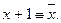
Рассмотрим использование данной операции в вопросе представления булевой функции единственным образом, наряду с совершенными формулами.
2. Полином Жегалкина.
Познакомимся с определением полинома:
Любую булеву функцию можно представить в виде двоичной суммы различных одночленов (конъюнкций), в которые все переменные входят не выше, чем в первой степени и константы 1 или 0, т.е. булева функция представима в виде:
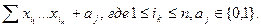

Причем, такое представление единственное.
Эта сумма называется многочленом Жегалкина.
Существует два способа представления булевой функции в виде полинома: метод неопределенных коэффициентов и метод построения полином по формуле. Опишем каждый метод подробно.
Метод неопределенных коэффициентов.
Перепишем полином в виде:
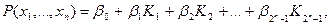 где Ki – конъюнкции, число которых равно 2n – 1,
где Ki – конъюнкции, число которых равно 2n – 1, 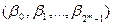 - вектор коэффициентов, где bI Î{0,1}.
- вектор коэффициентов, где bI Î{0,1}.
Коэффициент bI указывает на присутствие или отсутствие соответствующей конъюнкции в полиноме.
Алгоритм поиска вектора коэффициентов и составления полинома.
1. по таблице истинности составить систему уравнений 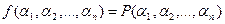 ,где (a1, a2, …, an) - все наборы значений переменных таблицы истинности для данной булевой функции (вместо переменных в полином подставить их соответствующие значения, в левой части уравнения – соответствующее этому набору значение функции).
,где (a1, a2, …, an) - все наборы значений переменных таблицы истинности для данной булевой функции (вместо переменных в полином подставить их соответствующие значения, в левой части уравнения – соответствующее этому набору значение функции).
3. пользуясь таблицей истинности для двоичного сложения и конъюнкции, вычислить коэффициенты bI;
4. подставить в полином значения коэффициентов и составить полином.
Представление булевой функции в виде полинома называется разложением функции в многочлен или в полином.
Рассмотрим пример.
Разложить функцию f(x, y, z) = (01101000).
Составим полином 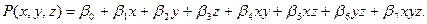
Cоставляя уравнения, нулевые конъюнкции будем исключать:
№1 = 23-3: (001): 0 = b0+ b3;
№2 = 23-2: (010): 1= b0+b2;
№3 = 23-2+23-3: (011): 1= b0+b2+b3+b6;
№4 = 23-1: (100): 0= b0+b1;
№5 = 23-1+23-3: (101): 1 = b0+b1+b3+b5;
№6 = 23-1+23-2: (110): 0 = b0+b1+b2+b4;
№7: (111): 0= b0+b1+b2+b3+b4+b5+b6+b7;
№8: (000): 0 = b0.
Решая систему, получим вектор коэффициентов: (0,0,1,0,1,1,0,1), тогда функция раскладывается в полином:
P(x,y,z) = 0 + y +xy + xz +xyz.
Проверку можно выполнить, составив таблицу истинности для полинома.
Построение полинома по формуле.
Данный метод основан на применении равносильных преобразований данной булевой функции, представленной в виде формулы, к виду полинома.
Алгоритм построения полинома по формул:
1. заменить формулу равносильной, содержащей только операции конъюнкцию и отрицание;
2. снять отрицания, пользуясь равносильностью: 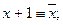
3. раскрыть скобки:
4. упростить, используя идемпотентность: х+х =0, равносильность х+0=х.
Рассмотрим примеры.
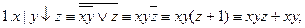
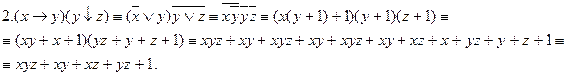
Задачи для самостоятельного решения.
1. Построить таблицу истинности для формулы 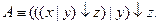 Составить для данной формулы КНФ и ДНФ.
Составить для данной формулы КНФ и ДНФ.
2. Методом неопределенных коэффициентов разложить функции в полиномы: а) f(x,y,z)= (01001110); б) f(x,y,z) = (11000101); в) f(x,y)= (0101); г) f(x,y)=(1011)
3. Методом неопределенных коэффициентов и путем равносильных преобразований построить полиномы для формул: а) х®у; б) (х|y)¯z; в) (x®y)(y¯z); г) ((x®y)v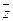 )|x.
)|x.
Контрольные вопросы
1. Привести таблицу истинности для штриха Шеффера. Выразить штрих Шеффера через отрицание и конъюнкцию. Выразить отрицание через штрих Шеффера.
2. Привести таблицу истинности для стрелки Пирса. Выразить стрелку Пирс через отрицание и дизъюнкцию. Выразить отрицание через стрелку Пирса.
3. Привести таблицу истинности для двоичного сложения. Выразить двоичное сложение через отрицание и эквиваленцию.
4. Перечислить свойства двоичного сложения.
5. Какое представление булевой функции называется полиномом Жегалкина?
6. Алгоритм построения полинома методом неопределенных коэффициентов.
7. Алгоритм построения полинома по формуле.
8. Сколько различных полиномов существует для одной булевой функции?
 2014-02-12
2014-02-12 6609
6609
