Лекция 10. 1. Полная система. Достаточное условие полноты

ТЕМА: ПОЛНОТА МНОЖЕСТВА ФУНКЦИЙ.

1. Полная система. Достаточное условие полноты.

2. Критерий полноты системы булевых функций.

3. Независимые системы. Базис замкнутого класса.

Главная

1. Полная система. Достаточное условие полноты.

Познакомясь с понятиями ДНФ, КНФ, СДНФ, СКНФ, полином Жегалкина выяснили, что любую булеву функцию можно выразить в виде формулы через элементарные функции: отрицание, конъюнкцию, дизъюнкцию, двоичное сложение и константу 0 или 1.

Эти функции можно рассматривать как систему элементарных функций, через которые выражается любая булева функция.

Возникает вопрос: в какой мере является случайным наличие таких систем элементарных функций?

Дадим определение таких систем.

Система булевых функций {f₁, f₂, …, f_m} называется полной, если любая булева функция может быть выражена через функции этой системы с помощью составления из них сложных функций.

Составление сложных функций из элементарных функций системы называется суперпозицией.

Познакомимся с достаточным условием полноты системы.

Пусть система функций {f₁, f₂, …, f_m} (I) полная и любая из функций этой системы может быть выражена через функции g₁, g₂, …, g_l, тогда система { g₁, g₂, …, g_l}(II) тоже полная.

Докажем полноту следующих систем: {-, V, L}, {-, V}, {-, L}, {-, ®}, {x|y}, {x¯y}, {0, 1, V, L, +}.

Полнота первой системы следует из того, что любую булеву функцию можно представить в виде ДНФ или КНФ.

Опираясь на достаточное условие полноты докажем, что вторая систем тоже полная. За полную систему примем {-, V, L}. Выразим функции этой системы через отрицание и дизъюнкцию. Нужно выразить только конъюнкцию: 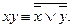следовательно, система {-, V} полная.

С помощью той же полной системы докажем полноту {-, L}. Для этого нужно выразить дизъюнкцию: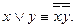

Для доказательства полноты системы {-, ®}воспользуемся полной системой {-, V}. Выразим дизъюнкцию: 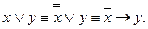Полнота доказана.

Для доказательства полноты системы {x|y} за полную примем, например, {-, L}. Выразим отрицание и конъюнкцию через штрих Шеффера:

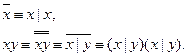
Полнота доказана.

При доказательстве полноты системы {x¯y} за полную систему примем {-, V}. Выразим обе функции через стрелку Пирса:

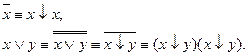
Полнота доказана.

Полноту системы можно доказать, опираясь на то, что любая булева функция представима в виде полинома, или доказав с помощью достаточного условия. Воспользуемся полной системой {-, L}. Выразим 0, 1 и + через отрицание и конъюнкцию:

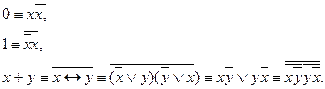
2. Критерий полноты системы булевых функций.

Мы рассмотрели лишь достаточное условие полноты системы. Перейдем теперь к установлению критерия полноты. Прежде познакомимся с понятиями замыкания и замкнутого класса.

Замыкание.

Пусть К – некоторое подмножество элементарных функций. Замыканием подмножества К называется множество булевых функций, представимых в виде формул через функции К. Обозначение замыкания: [K].

Пример: замыканием множества булевых функций является само это множество. Обозначим множество всех булевых функций через Р₂ (2- так как функция принимает только два значения). Тогда [P₂]= P₂.

Свойства замыкания:

1. KÍ [K];

2. если K₁Í K₂, то [K₁]Í [K₂];

3. [K₁]È[K₂]Í[K₁ÈK₂].

Можно теперь сформулировать еще одно определение полной системы:

К – полная система, если ее замыкание- все булевы функции.

Замкнутый класс.

Множество К называется функционально замкнутым (или просто замкнутым), если его замыкание – само множество К..

Дадим еще одно определение замкнутого множества (класса).

Класс К булевых функций называется замкнутым, если вместе с функциями из этого класса он содержит и все их суперпозиции, т.е. элементарные суперпозиции не выводят из этого класса. К элементарным суперпозициям относятся:

1. переименование некоторой переменной какой-нибудь функции рассматриваемой системы;

2. подстановка некоторой функции из этой системы вместо некоторой переменной любой из функции этой системы.

К замкнутым классам относятся: множество всех булевых функций Р₂; класс функций от одной переменной; класс, содержащий только тождественные функции вида f(X)=X.

Приведем следующее утверждение:

Никакая полная система функций не может содержаться в функционально замкнутом классе, отличном от класса Р₂ всех булевых функций.

Действительно, в противном случае найдется замкнутый класс К такой, что {f₁, f₂, …, f_m}ÌКÌР₂ и К¹Р₂. значит, найдется функция f такая, что fÏК, т.е. не может быть выражена через {f₁, f₂, …, f_m}, что противоречит полноте этой системы.

Рассмотрим некоторые функционально замкнутые классы функций, которые называются важнейшими замкнутыми классами. Они используются в критерии полноты.

Класс Т₀ – класс функций, сохраняющих 0, т.е. f(0,0,…0)=0.

Примеры функций, принадлежащих к Т₀: 0, х, ху=00=0, xvy=0v0=0, x+y=0+0=0.

Функции, не принадлежащие к Т₀: 1, x|y=0|0=1, x¯y=0¯0=1.

Класс Т₁- класс функций, сохраняющих 1, т.е. f(1,1,…,1)=1.

К этому классу относятся, например, 1, x, xy=11=1, xvy=1v1=1, x®y=1®1=1.

Примеры функций, не принадлежащих классу Т₁: 0, x|y=1|1=0, x¯y=1¯1=0.

Класс S – класс самодвойственных функций.

Самодвойственной функцией называется функция f(x₁, x₂, …,x_n), если f(x₁, x₂, …,x_n) º f*(x₁, x₂, …,x_n), где .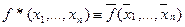

К S относится, например, :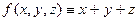

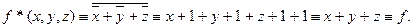
Функции ху, xvy, x®y не относятся к самодвойственным функциям.

Класс L – класс линейных функций.

Функция называется линейной, если равносильная ей функция, являющаяся полиномом содержит конъюнкции не выше первой степени, т. е.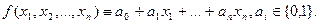

К линейным относятся: 1, 0, х, 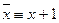, х+у.

Функции 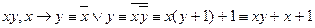не линейные.

Класс монотонных функций M.

Введем отношение частичного порядка на множестве упорядоченных наборов (векторов).

Вектор a= (a₁, a₂,…,a_n) предшествует вектору b = (b₁, b₂,…, b_n), если a_i £ b_i для любых i= 1 – n. Обозначение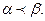

Например, 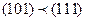, т.к. 1£1, 0 £ 1, 1 £ 1. векторы (01) и (10) – не сравнимы.

Говорят так же, что a и b сравнимы.

Функция f(x₁, x₂, …,x_n) называется монотонной, если любых векторов a и b списка переменных таких, что 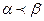, имеем f(a)£ f(b).

К монотонным относятся, например, функции: х, ху, xvy.

Проверим монотонность xy и xvy. Составим таблицы истинности:

х	у	ху

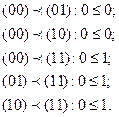
х	у	хvу

По таблице истинности легко установить монотонность и этой функции.

Функция х®у не является монотонной, т.к. 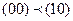, но f(00)=1, a f(10)=0.

Любые элементарные суперпозиции не выводят из рассмотренных классов. Тем самым доказывается их функциональная замкнутость.

Чтобы доказать полноту какой-либо системы, оказывается, можно ограничится рассмотренными пятью классами. Итак, рассмотрим критерий полноты (теорему Поста), который является необходимым и достаточным условием полноты системы булевых функций.

Для того, чтобы система булевых функций была полной, необходимо и достаточно, чтобы для каждого из классов Т₀, Т₁, S, L, M нашлась функция f_i из этой системы не принадлежащая этому классу.

Для доказательства полноты с помощью теоремы Поста, нужно составить таблицу, которая называется таблицей Поста: по горизонтали перечислены замкнутые классы, по вертикали – функции системы. В ячейке ставят минус, если функция не принадлежит классу, и плюс, если принадлежит.

Рассмотрим пример: докажем полноту системы {+, v, 1,0}.

Составим таблицу:

f	T0	T1	S	L	M
x+y	+	-	-	+	-
xvy	+	+	-	-	+
	-	+	-	+	+
	+	-	-	+	+

Для 0 и 1 таблица заполняется тривиально. Не составляет труда проверить принадлежность х+у и xvy к Т₀ и Т₁. Более подробно покажем заполнение оставшихся ячеек.

Для функции х+у.

S: 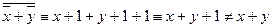, значит, х+уÏS;

L: x+yÎL;

M: составим таблицу истинности:

х	у	х+у

Функция не монотонная, т.к., например, 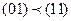, а f(01)>f(11).

Для функции xvy.

S: для xvy двойственной является ху, следовательно, х+уÏS;

L: 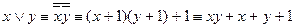, значит, xvyÏL;

Принадлежность этой функции мы уже доказали в выше рассмотренном примере.

Итак, т.к. в каждом столбце есть хотя бы один минус, означает полноту данной системы.

3. Независимые системы. Базис замкнутого класса.

Система функций G называется независимой, если никакая функция fÎG не представима суперпозициями функций из G\f.

Примеры независимых систем:

{L, -}, {V, -}.

Система {L, V, -} не является независимой, т.к. удалив V или L,получим систему, суперпозициями функций которой можно представить любую из функций системы {L, V, -}.

Независимая система функций G называется базисом замкнутого класса К, если всякая функция из К есть суперпозиция функций из G.

Например, системы {-, V}, {-, L} являются базисом для класса Р₂, т.к. системы полные и независимые.

Система {+, v, 1,0} не является базисом для Р₂, т.к. хотя она полная, но не является независимой: можно удалить 0. значит базисом для Р₂ является система {+, v, 1}.

Функции, образующие базис во множестве всех булевых функций Р₂, называются шефферовыми функциями.

Например, функции x|y и х¯у – шефферовые, т.к. каждая из них образует полную систему (было доказано выше), причем, независимую.

Функция х®у не является шефферовой, т. к. не образует полную систему: 1®1=1, т.е. х®уÎТ₁.

Задачи для самостоятельного решения.

1. Выразить импликацию через функции системы {1, +, L}.

2. Выразить дизъюнкцию и конъюнкцию через функции системы {-, ®}.

3. С помощью достаточного условия полноты проверить на полноту систему а) {0, v, ®}; б) {-, «}; в) {0, +, L}.

4. С помощью теоремы Поста проверить на полноту системы: {+, V, L, -}, {L, ®, -}, {«, -}, {1, 0, -}.

5. Является ли система {1,0,+,L} базисом множества всех булевых функций?

6. Являются ли функции х«у, ху, xvy, 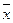шефферовыми функциями?

Контрольные вопросы

1. Что называется замыканием множества булевых функций?

2. Перечислить свойства замыкания.

3. Что такое суперпозиция? Какие суперпозиции относятся к элементарным?

4. Сформулировать два определения функционально замкнутого класса.

5. Сформулировать и доказать утверждение о принадлежности полной системы только к замкнутому классу Р₂ .

6. Перечислить все важнейшие замкнутые классы. Привести примеры функций принадлежащих и не принадлежащих к каждому замкнутому классу.

7. Сформулировать теорему Поста. Что собой представляет таблица Поста?

8. Какая система булевых функций называется независимой?

9. Что такое базис замкнутого класса?

10. Какие функции называются шефферовыми?