Лекция 15. 1. Сформулировать принцип метода математической индукции

Контрольные вопросы

1. Сформулировать принцип метода математической индукции.

2. Сформулировать обобщенный метод математической индукции.

3. Вычислить сумму: 2+ 4+ 6+…+2n.

4. Вычислить сумму: 1+3+5+…+(2n-1).

5. Доказать справедливость равенства: 1²+3²+5²+…+(2n-1)² =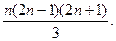

6. Доказать справедливость неравенства: 2ⁿ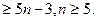

7. Докажите, что истинно высказывание: 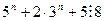при любых натуральных n.

8. Доказать справедливость неравенства: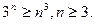

ТЕМА: БИНАРНЫЕ ОТНОШЕНИЯ.

ПЛАН:

1. Понятие отношения. Бинарное отношение

2. Операции над бинарными отношениями

3. Свойства бинарных отношений

4. Специальные бинарные отношения

Главная

1. Понятие отношения. Бинарное отношение.

Пусть заданы множества Х₁, Х₂,…,Х_n и рассматривается некоторое подмножество их прямого произведения rÌ Х₁Х₂…Х_n, т.е. множество упорядоченных наборов (а₁, а₂,…,а_n), где а₁ÎХ₁, а₂ÎХ₂,…,а_nÎХ_n. Это множество называется n – местным отношением или n –арным предикатом, заданном на множестве Х₁Х₂…Х_n.Если Х₁= Х₂=…=Х_n=М, то rÌ Мⁿ и называется n – местным отношением на множестве М.

Пример: на множестве R³ задан трехместный предикат или трехместное отношение P(x, y, z): «x²+y²+z²=25».

Говорят что а₁, а₂,…,а_n находятся в отношении r, если (а₁, а₂,…,а_n)Ì r.

Наиболее хорошо изучены двухместные отношения, которые называются бинарными. Приведем определение бинарных отношений, опираясь на определение n – местного отношения.

Пусть даны непустые множества Х и У, и подмножество их прямого произведения rÌ ХУ. r называется бинарным отношением.

Т.е. r - множество упорядоченных пар (х, у). Говорят, что х и у находятся в отношении r, если (х, у) Ì r. Допускается запись: х r у, означающая, что (х, у) Ì r.

Элементы х и у называются координатами или компонентами отношения r.

Область определения бинарного отношения r называется множество Dr = {x| существует такое у, что х r у}.

Областью значений бинарного отношения r называется множество Rr = {y| существует такое х, что х r у}.

Понятие отношения следует рассматривать, как естественное обобщение знакомых нам отношений из математики и из жизненных представлений.

Рассмотрим некоторые примеры бинарных отношений.

1. Отношения на множестве натуральных чисел N:

а) «х £ у», например, пары (7,7) и (6,8) принадлежат этому отношению, а пара (8,6) – не принадлежит. Область определения Dr =N, область значений Rr=N;

б) «иметь общий делитель, не равный единице». Пары (6,9), (4,2), (4,4) принадлежат этому отношению, а пары (7,9), (5,8) – не принадлежат. Область определения Dr =N, область значений Rr=N.

2. Отношение равенства на множестве действительных чисел R: «х = у». Этому отношению принадлежат все пары, в которых координаты равны, например, (9,9), (2,3; 2,3). Область определения Dr =R, область значений Rr=R.

3. Отношения на множестве точек декартовой плоскости:

а) «находится на одинаковом расстоянии от начала координат» - это множество всех пар (х,у), где хÎR и уÎR, таких, что х² + у² = r², т.е. все точки окружности с центром в начале координат и радиусом r;

б) «быть симметричными относительно оси х» - этому отношению принадлежат пары точек (х,у) и (х,-у).

4. Отношения на множестве людей:

а) «жить в одном городе»;

б) «быть старше (моложе);

в) «быть сыном»;

г) «быть знакомыми».

2. Операции над бинарными отношениями.

Для бинарных отношений определены теоретико – множественные операции объединения, пересечения и так далее.

Кроме этих операций над бинарными отношениями производят следующие оперции.

Обратное отношение. Для отношения r обратным является отношение r^-1={(x,y)|(y,x)Îr}.

Для отношения х ³ у обратным является х £ у. Для отношения «быть делителем» обратное- «быть кратным».

Композицией отношений r₁ и r₂ называется отношение r₂оr₁ = {(x,z)| существует у такое, что (х,у) Îr₁ и (у,z) Îr₂ }.

Композицией двух отношений «Нина дочь Людмилы Ивановны» и «Людмила Ивановна мать Сергея» является отношение «Нина сестра Сергея».

Композицией двух отношений «прямая проходит через точку» и «точка принадлежит плоскости» является отношение «прямая пересекает плоскость».

Для любых бинарных отношений выполняются следующие свойства:

1. (r^-1)^-1=r. это свойство следует из определения обратного отношения;

2. (r₂оr₁)^-1 = r₁^-1оr₂^-1.

Для доказательства второго свойства, покажем, что множества в обеих частях равенства состоят из одних и тех элементов: (х,у)Î (r₂оr₁)^-1«(у,х)Î r₂оr₁«$z (y,z)Îr₁ и (z,x)Îr₂«$z (y,z)Îr₁^-1 и (x,z))Îr₂^-1«(x,y)Î r₁^-1оr₂^-1.