Обобщение метода математической индукции

Бывают случаи, когда утверждение, неверное для n =1, 2,..., р - 1, справедливо для n = р.Если затем из предположения о его истинности для n = k>pможно доказать, что оно истинно и для n = k +1, то получаем, что данное выражение истинно для всех n ³ р.

Пример 6. Докажем, что выражение 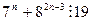(кратно 19) для всех натуральных чисел n ³ 3.

Решение. При n = 3 получаем

7³ + 8^2×3-3 = 343 + 512 = 855 = 45× 19

т. е. при n = 3 утверждение верно.

Предположим, что 7^k +8^2k-3 кратно 19 при k >3, и докажем, что 7^k+1 + 8^2(k+1)-3 кратно 19.

По предположению 7^k +8^2k-3 = 19m, где mÎN,значит,

8^2k-3 = 19m – 7^k.

Отсюда имеем:

7^k+1 + 8^2(k+1)-3 = 7^k+1 + 8^2k-3+2 = 7^k+1 + 64×8^2k-3 = 7^k+1 + 64(19m – 7^k) = 7^k(7 – 64) + 64× 19m = 64 × 19m – 57 × 7^k = 19(64m - 3×7^k),

т. е. выражение кратно 19.

Итак, мы доказали, что утверждение верно для n = 3, и из предположения, что оно верно для n = k>3,доказали его спра­ведливость для n = k + 1. Тогда на основании сказанного выше заключаем, что выражение 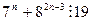для всех n ³ 3.

Пример 7. Доказать, что 2ⁿ ³ 5n – 3 при n ³ 5.

При n = 5: 2⁵ = 32, 5×5 – 3 = 22 и 32 > 22.

Пусть неравенство верно при n = k, k > 5, т.е. 2^k ³ 5k – 3.

Докажем справедливость неравенства при n = k +1, т.е. справедливость неравенства 2^k+1 ³ 5(k+1) – 3 или 2^k+1 ³ 5k +2.

Умножим обе части неравенства на 2: 2^k+1 ³ 2(5k – 3).

Преобразуем правую часть неравенства: 2(5k – 3) = 10k – 6 = 5k + 2 + 5k – 8. Заметим, что 5k – 8 ³ 0 при k > 5, тогда 5k + 2 + 5k – 8 > 5k + 2 и, тогда 2^k+1 ³ 5k +2.