Предыдущие выкладки показывают, что если  - какая-нибудь правильная рациональная дробь, разложение которой на простейшие дроби есть
- какая-нибудь правильная рациональная дробь, разложение которой на простейшие дроби есть
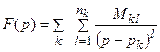
то
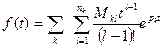 (21.20)
(21.20)
будет оригиналом, имеющим изображение  .
.
В частности, если все полюсы  - простые, то
- простые, то
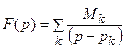 ;
; 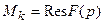 ,
,
и для оригинала, имеющего изображение  , получим формулу
, получим формулу
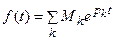 (21.21)
(21.21)
Заметимеще, что если
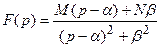 (21.22)
(21.22)
то соответствующим оригиналом будет
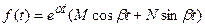 (21.23)
(21.23)
Таким образом, нахождение оригинала по заданному рациональному изображению сводится к разложению правильной рациональной дроби на простейшие дроби.
Пример 21.1. Найти оригинал  , имеющий изображение
, имеющий изображение
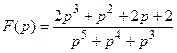 .
.
Разложим это изображение на простейшие дроби:
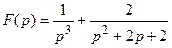 .
.
Первое слагаемое в полученном изображении можно умножить и разделить на 2: 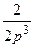 , т.к.
, т.к. 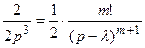 при
при 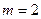 и
и 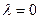 . Учитывая формулу (1.8), запишем оригинал этого изображения:
. Учитывая формулу (1.8), запишем оригинал этого изображения:
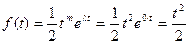 ≒
≒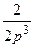 .
.
Второе слагаемое представим в виде: 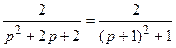 , которое соответствует виду изображения (21.22) -
, которое соответствует виду изображения (21.22) - 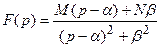 , при
, при 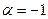 ,
, 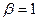 ,
, 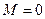 и
и 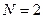 . Учитывая формулу (21.23), запишем оригинал этого изображения:
. Учитывая формулу (21.23), запишем оригинал этого изображения: 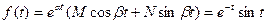 ≒
≒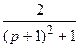 .
.
Таким образом, окончательный вид оригинала, соответствующий исходному изображению, будет:
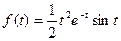 ≒
≒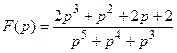 .
.
Пример 21.2. Найти оригинал  , имеющий изображение
, имеющий изображение 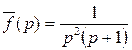 .
.
Рассмотрим два метода.
1. Разложение изображения на сумму изображений.
Представим исходное изображение в виде суммы простых дробей
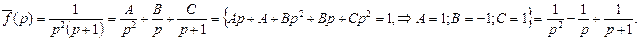
С учетом того, что
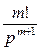 ≒ tm, то при m = 1, будем иметь
≒ tm, то при m = 1, будем иметь 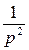 ≒ t и
≒ t и 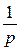 ≒1;
≒1;
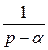 ≒
≒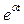 , то при α = -1, будем иметь
, то при α = -1, будем иметь 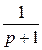 ≒ e-t.
≒ e-t.
Следовательно, изображение 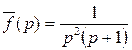 имеет оригинал вида t -1+ e-t, т.е.
имеет оригинал вида t -1+ e-t, т.е.
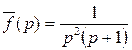 ≒ t -1+ e-t.
≒ t -1+ e-t.
2. Разложение изображения на произведение изображений.
Обозначим
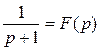 ≒ e-t = f 1 (t) и
≒ e-t = f 1 (t) и 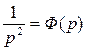 ≒ t = f 2 (t).
≒ t = f 2 (t).
Применив формулу Дюамеля 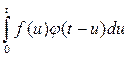 ≒
≒ 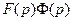 , получим
, получим
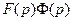 ≒
≒ 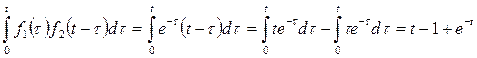
Следовательно, изображение 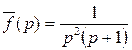 имеет оригинал вида t -1+ e-t, т.е.
имеет оригинал вида t -1+ e-t, т.е.
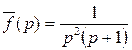 ≒ t -1+ e-t.
≒ t -1+ e-t.
Пример 21.3. Найти оригинал  , имеющий изображение
, имеющий изображение 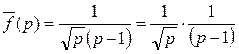 .
.
Обозначим
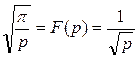 ≒
≒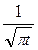 = f 1 (t) и
= f 1 (t) и 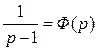 ≒ et = f 2 (t).
≒ et = f 2 (t).
Применив формулу Дюамеля 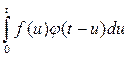 ≒
≒ 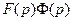 , получим
, получим
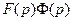 ≒
≒ 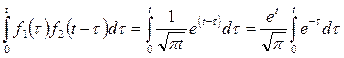
Следовательно, изображение 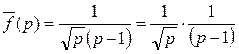 имеет оригинал вида
имеет оригинал вида 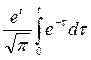 , т.е.
, т.е.
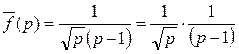 ≒
≒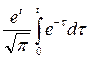 .
.
 2014-02-12
2014-02-12 3600
3600
